题目内容
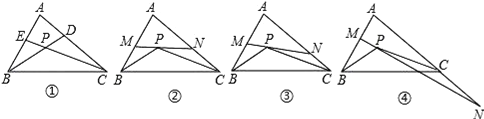
【题目】如图①,△ABC的角平分线BD,CE相交于点P.
(1)如果∠A=80,求∠BPC= .
(2)如图②,过点P作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示) .
(3)将直线MN绕点P旋转。
(i)当直线MN与AB,AC的交点仍分别在线段AB和AC上时,如图③,试探索∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。
(ii)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(i)中∠MPB,∠NPC,∠A三者之间的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请给出∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由。

【答案】130°;
(2)90°﹣![]() ∠A
∠A
(3)(i)∠MPB+∠NPC=90°﹣![]() ∠A,理由见解析.
∠A,理由见解析.
(ii)不成立,有∠MPB﹣∠NPC=90°﹣![]() ∠A.
∠A.
理由见解析.
【解析】试题分析: (1)根据三角形内角和定理得到![]() ,再根据角平分线定义得到
,再根据角平分线定义得到![]() ,再利用三角形内角和定理得
,再利用三角形内角和定理得![]() ,然后把∠A的度数代入计算;
,然后把∠A的度数代入计算;
(2)根据平角定义得![]() ,然后根据(1)的求解;
,然后根据(1)的求解;
(3)( i)∠与(2)的说理一样;
(ⅱ)有结论![]() .
.
本题解析:(1) ![]()
![]()
![]()
![]()
![]() 故答案为:
故答案为: ![]()
(2)由![]() =
= ![]() 得∠MPB+∠NPC=
得∠MPB+∠NPC=![]() ∠BPC=
∠BPC=![]() 1(
1(![]() +
+![]() ∠A)=
∠A)= ![]()
![]() ∠A;故答案为:∠MPB+∠NPC=
∠A;故答案为:∠MPB+∠NPC=![]()
![]() ∠A.
∠A.
(3)(i)∠MPB+∠NPC=![]()
![]() ∠A.
∠A.
理由如下:
∵∠BPC=![]() +12∠
+12∠![]() A,
A,
∴∠MPB+∠NPC=![]() ∠BPC=180(
∠BPC=180(![]() +
+![]() ∠A)=
∠A)= ![]() 12
12![]() ∠A.
∠A.
(ii)不成立,有∠MPB∠NPC=![]()
![]() ∠A.
∠A.
理由如下:由题图④可知∠MPB+∠BPC∠NPC=![]() ,
,
由(1)知:∠BPC=![]() +
+![]() ∠A,∴∠MPB∠NPC=
∠A,∴∠MPB∠NPC=![]() ∠BPC=
∠BPC=![]() (
(![]() +
+![]() ∠A)=
∠A)= ![]()
![]() ∠A.
∠A.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
