题目内容
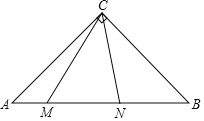
【题目】如图,在Rt△ABC中,∠ACB=90°,CA=CB,M,N分别AB上的两动点,且∠MCN=45°,下列结论:①![]() ;②CM2﹣CN2=NBNA﹣MBMA;③AM2+BN2=MN2;④S△CAM+S△CBN=S△CMN,其中正确的有( )
;②CM2﹣CN2=NBNA﹣MBMA;③AM2+BN2=MN2;④S△CAM+S△CBN=S△CMN,其中正确的有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①由勾股定理即可得![]() ;
;
②过点C作CD⊥AB于D,由等腰直角三角形性质可得AD=BD=CD,再由勾股定理即可得CM2-CN2=NBNA-MBMA;
③过点B作BM′⊥AB,使BM′=AM,连接CM′,M′N,可证:△CBM′≌△CAM,△M′CN≌△MCN,再由勾股定理可得:M′B2+BN2=M′N2,即AM2+BN2=MN2;
④由全等三角形面积相等可知:S△CBM′=S△CAM,S△CNM′=S△MCN,即可得S△CAM+S△CBN>S△MCN.
解:①在Rt△ABC中,∠ACB=90°,CA=CB,
AB![]() AC,
AC,
故①正确;
②如图1,过点C作CD⊥AB于D.

∵∠ACB=90°,CA=CB,CD⊥AB,
∴AD=BD=CD
CM2=CD2+MD2,CN2=CD2+DN2,
∴CM2﹣CN2=MD2﹣DN2=(MD+DN)(MD﹣DN)=MN(MD﹣DN)=MN(MB﹣NA)
∵NBNA﹣MBMA=NBNA﹣MB(NA﹣MN)
=MBMN+NBNA﹣MBNA
=MBMN﹣NA(MB﹣NB)
=MBMN﹣NAMN
=MN(MB﹣NA),
∴CM2﹣CN2=NBNA﹣MBMA
故②正确;
③如图2,过点B作BM′⊥AB,使BM′=AM,连接CM′,M′N,则∠ABM′=90°
∵∠ACB=90°,CA=CB,
∴∠A=∠ABC=45°,
∴∠CBM′=45°=∠A
在△CBM′和△CAM中
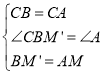 ,
,
∴△CBM′≌△CAM(SAS),
∴CM′=CM ∠BCM′=∠ACM,
∴∠M′CN=∠BCM′+∠BCN=∠ACM+∠BCN=∠ACB-∠MCN=90°-45°=45°=∠MCN
在△M′CN和△MCN中
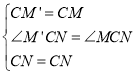 ,
,
∴△M′CN≌△MCN(SAS),
∴M′N=MN
在Rt△M′BN中,∠M′BN=90°,M′B2+BN2= M′N2,
∴AM2+BN2=MN2
故③正确;
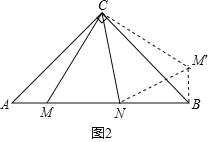
④如图2.
∵△CB M′≌△CAM,△M′CN≌△MCN,
∴S△CBM′=S△CAM,S△CNM′span>=S△MCN,
∴S△CAM+S△CBN=S△CBM′+S△CBN=S△CNM′+S△BNM′=S△MCN+S△BNM′>S△MCN,
故④错误.
故选:C.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案