��Ŀ����
����Ŀ��ij�̳���A��B������Ʒ������2��A��Ʒ��1��B��Ʒ������80Ԫ������3��A��Ʒ��2��B��Ʒ������135Ԫ��
��1����A��B������Ʒÿ���ۼ۷ֱ�ΪaԪ��bԪ����a��b��ֵ��
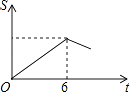
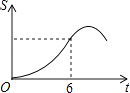
��2��B��Ʒÿ���ijɱ���20Ԫ�������г����飺������1��������ĵ������ۣ����̳�ÿ������B��Ʒ100���������۵���ÿ����1Ԫ��B��Ʒÿ����������ͼ���5���� ����ÿ��B��Ʒ����������y��Ԫ�������۵��ۣ�x��Ԫ֮��ĺ�����ϵ��
�������۵���Ϊ����Ԫʱ��B��Ʒÿ����������������������Ƕ��٣�
���𰸡�
��1���⣺��������ã� ![]() ��
��
��ã� ![]()
��2���⣺��������ã�y=��x��20����100��5��x��30����
��y=��5x2+350x��5000��
�ڡ�y=��5x2+350x��5000=��5��x��35��2+1125��
�൱x=35ʱ��y���=1125��
�����۵���Ϊ35Ԫʱ��B��Ʒÿ�����������������������1125Ԫ
����������1�����������з����鼴�ɵõ����ۣ���2�����������г�����x��y�ķ��̼��ɣ��ڰѺ�����ϵʽ�䷽���ɵõ������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��Ϊ�˽�ij����������õ����������Ը�����10��������е��飬�±�����10������2015��4�·��õ����ĵ�������
������ | 1 | 2 | 3 | 4 |
���õ�������/���� | 30 | 42 | 50 | 51 |
��ô������10���������õ�������λ���ȣ�������˵��������ǣ� ��
A.�����50
B.������51
C.������42
D.������21