Question

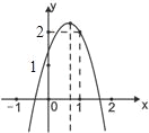
【题目】如图①，二次函数的抛物线的顶点坐标C，与x轴的交于A（1，0）、B（﹣3，0）两点，与y轴交于点D（0，3）．

（1）求这个抛物线的解析式；

（2）如图②，过点A的直线与抛物线交于点E，交y轴于点F，其中点E的横坐标为﹣2，若直线PQ为抛物线的对称轴，点G为直线PQ上的一动点，则x轴上是否存在一点H，使D、G、H、F四点所围成的四边形周长最小？若存在，求出这个最小值及点G、H的坐标；若不存在，请说明理由；

（3）如图③，连接AC交y轴于M，在x轴上是否存在点P，使以P、C、M为顶点的三角形与△AOM相似？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】

【1】 设所求抛物线的解析式为：,将A(1,0)、B(-3,0)、 D（0,3）代入，得…………………………………………2分

即所求抛物线的解析式为：……………………………3分

【2】 如图④，在y轴的负半轴上取一点I，使得点F与点I关于x轴对称，

在x轴上取一点H，连接HF、HI、HG、GD、GE，则HF＝HI…………………①

设过A、E两点的一次函数解析式为：y＝kx＋b（k≠0），

∵点E在抛物线上且点E的横坐标为-2，将x＝-2，代入抛物线，得

∴点E坐标为（-2，3）………………………………………………………………4分

又∵抛物线图象分别与x轴、y轴交于点A(1,0)、B(-3,0)、

D（0，3），所以顶点C（-1,4）

∴抛物线的对称轴直线PQ为：直线x＝-1， [中国教#&~@育出%版网]

∴点D与点E关于PQ对称，GD＝GE……………………………………………②

分别将点A（1，0）、点E（-2，3）

代入y＝kx＋b，得：

解得：

过A、E两点的一次函数解析式为：

y＝-x＋1

∴当x＝0时，y＝1

∴点F坐标为（0，1）……………………5分

∴=2………………………………………③

又∵点F与点I关于x轴对称，

∴点I坐标为（0，-1）

∴……………………………………④

又∵要使四边形DFHG的周长最小，由于DF是一个定值，

∴只要使DG＋GH＋HI最小即可 ……………………………………6分

由图形的对称性和①、②、③，可知，

DG＋GH＋HF＝EG＋GH＋HI

只有当EI为一条直线时，EG＋GH＋HI最小

设过E（-2，3）、I（0，-1）两点的函数解析式为：，

分别将点E（-2，3）、点I（0，-1）代入，得：

解得：

过I、E两点的一次函数解析式为：y＝-2x-1

∴当x＝-1时，y＝1；当y＝0时，x＝-；

∴点G坐标为（-1，1），点H坐标为（-，0）

∴四边形DFHG的周长最小为：DF＋DG＋GH＋HF＝DF＋EI

由③和④，可知：

DF＋EI＝

∴四边形DFHG的周长最小为. …………………………………………7分

【3】 如图⑤，

由(2)可知，点A(1,0)，点C（-1,4），设过A(1,0)，点C（-1,4）两点的函数解析式为：，得：

解得：，

过A、C两点的一次函数解析式为：y＝-2x+2,当x＝0时，y＝2，即M的坐标为（0,2）；

由图可知，△AOM为直角三角形，且， ………………8分

要使，△AOM与△PCM相似，只要使△PCM为直角三角形，且两直角边之比为1:2即可，设P(,0)，CM=，且∠CPM不可能为90°时，因此可分两种情况讨论； ……………………………………………………………………………9分

①当∠CMP=90°时，CM=，若则，可求的P（-4,0），则CP=5，，即P（-4,0）成立，若由图可判断不成立；……………………………………………………………………………………10分

②当∠PCM=90°时，CM=，若则，可求出

P（-3,0），则PM=，显然不成立，若则，更不可能成立.……11分

综上所述，存在以P、C、M为顶点的三角形与△AOM相似，点P的坐标为（-4,0）12分

【解析】

(1)直接利用三点式求出二次函数的解析式；

（2）若四边形DFHG的周长最小，应将边长进行转换，利用对称性，要使四边形DFHG的周长最小，由于DF是一个定值，只要使DG＋GH＋HI最小即可，

由图形的对称性和，可知，HF＝HI，GD＝GE，

DG＋GH＋HF＝EG＋GH＋HI

只有当EI为一条直线时，EG＋GH＋HI最小，即

，DF＋EI＝

即边形DFHG的周长最小为.

（3）要使△AOM与△PCM相似，只要使△PCM为直角三角形，且两直角边之比为1:2即可，设P(,0)，CM=，且∠CPM不可能为90°时，因此可分两种情况讨论，①当∠CMP=90°时，CM=，若则，可求的P（-4,0），则CP=5，，即P（-4,0）成立，若由图可判断不成立；②当∠PCM=90°时，CM=，若则，可求出P（-3,0），则PM=，显然不成立，若则，更不可能成立. 即求出以P、C、M为顶点的三角形与△AOM相似的P的坐标（-4，0）