题目内容
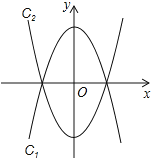
【题目】将抛物线c1: ![]() 沿x轴翻折,得到抛物线c2,如图1所示.
沿x轴翻折,得到抛物线c2,如图1所示.
(1)请直接写出抛物线c2的表达式;
(2)现将抛物线c1向左平移m个单位长度,平移后得到新抛物线的顶点为M,与x轴的交点从左到右依次为A、B;将抛物线c2向右也平移m个单位长度,平移后得到新抛物线的顶点为N,与![]() 轴的交点从左到右依次为D、E.
轴的交点从左到右依次为D、E.
①当B、D是线段AE的三等分点时,求m的值;
②在平移过程中,是否存在以点A、N、E、M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.
【答案】(1)![]() (2)①2,1/2,②是矩形,m=1
(2)①2,1/2,②是矩形,m=1
【解析】试题分析:因为二次函数的图像关于x轴对称时,函数中的a,c,互为相反数,b值不变,函数向左平移时,纵坐标不变,横坐标均减少平移个单位,可假定成立,由直角三角形性质得到验证。解:(1)抛物线c2的表达式是![]() ; 2分;
; 2分;

(2)①点A的坐标是(![]() ,0), 3分;
,0), 3分;
点E的坐标是(![]() ,0). 4分;
,0). 4分;
②假设在平移过程中,存在以点A,M,E为顶点的三角形是直角三角形.
由题意得只能是![]() .
.
过点M作MG⊥x轴于点G.
由平移得:
点M的坐标是(![]() ,
, ![]() ), 5分;
), 5分;
∴点G的坐标是(![]() ,0),
,0),
∴![]() ,
, ![]() ,
,
![]() ,
,
在Rt△AGM中,
∵ tan![]() ,
,
∴![]() , 6分;
, 6分;
∵![]() ,
,
∴![]() ,
,
∴tan![]() ,
,
∴![]() , 7分;
, 7分;
∴![]() . 8分.
. 8分.
所以在平移过程中,当![]() 时,存在以点A,M,E为顶点的三角形是直角三角形.
时,存在以点A,M,E为顶点的三角形是直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目