Question

【题目】阅读下列两段材料，回答问题：

材料一:A（x1．y1)，B(x2．y2)的中点坐标为(，) 例如，点(1，5)，(3，-1)的中点坐标为(，)，即(2， 2)

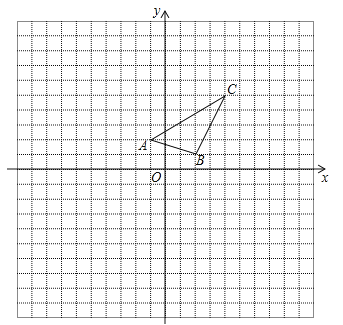
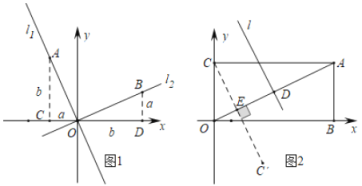
材料二：如图1，正比例函数l1:y=k1x和l2:y=k2x的图像相互垂直，分别在l1和l2上取点A、B，使得AO=BO．分别过点A、B作x轴的垂线，垂足分别为点C、D．显然△AOC≌△ OBD．设OC=BD=a，AC=OD=b．则A（-a，b），B(b，a)．于是，所以k1k2的值为一个常数．

（1）在材料二中，k1k2=____ (写出这个常数具体的值) ；

（2）如图，在矩形OBAC中A（4，2），点D是OA中点，用两段材料的结论，求点D的坐标和OA的垂直平分线l的解析式；

（3）若点C’ 与点C关于OA对称，用两段材料的结论，求点C'的坐标，

Answer 1

【答案】（1）-1；（2）D(2，1)，OA的垂直平分线l的解析式为：y=-2x+5；（3）C′()．

【解析】

（1）根据材料二中，，即可得到答案；

（2）根据线段中点坐标公式，可得D的坐标，求出直线OA的解析式为：y=x，可设OA的垂直平分线l的解析式为：y=-2x+b，根据待定系数法，即可得到答案；

（3）由C，C′关于OA对称，可设CC′所在直线的解析式为：y=-2x+b，根据待定系数法，即可求出CC′所在直线的解析式，进而求出E的坐标，根据中点坐标公式，即可得到C′的坐标．

（1）∵，

∴k1k2=-1，

故答案是：-1；

（2）∵O(0，0)，A(4，2)，

∴D()，即：D(2，1)，

设直线OA的解析式为：y=kx，

把A(4，2)代入得：2=4k，解得：k=，

∴直线OA的解析式为：y=x，

设OA的垂直平分线l的解析式为：y=-2x+b，

把D(2，1)代入得：1=-2×2+b，解得：b=5，

∴OA的垂直平分线l的解析式为：y=-2x+5；

（3）∵C，C′关于OA对称，

∴CC′⊥OA，E是CC′的中点，

设CC′所在直线的解析式为：y=-2x+b，

把C(0，2)代入解析式得：b=2，

∴CC′所在直线的解析式为：y=-2x+2，

联立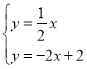，解得：，

∴E()，

∴C′()，即：C′()．