Question

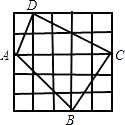
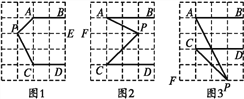
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,已知AB∥CD,分别探讨下面三个图形中∠BAP与∠APC,∠DCP的关系,请任选一个加以说明.

Answer 1

【答案】见解析

【解析】试题分析：(1)过P作AB平行线，利用同旁内角关系证明.(2) 过P作AB平行线，利用内错角关系证明.（3）过P作AB平行线，利用内错角关系证明.

试题解析：

对图1,∠BAP+∠DCP+∠APC=360°.

证明:过P作PE∥AB,

则AB∥CD,

因为AB∥PE,所以∠PAB+∠APE=180°,

因为PE∥CD,所以∠DCP+∠CPE=180°,

所以∠PAB+∠APE+∠DCP+∠CPE=360°,

即∠BAP+∠DCP+∠APC=360°,

对图2,∠BAP+∠DCP=∠APC,

证明:过P作PF∥AB,则PF∥CD.

因为PF∥AB,

所以∠APF=∠BAP,

同理∠CPF=∠DCP,

又因为∠APC=∠APF+∠CPF,

所以∠BAP+∠DCP=∠APC,

对图3,∠BAP-∠DCP=∠APC,

证明:过P作PF∥AB,则PF∥CD,

因为PF∥AB,

所以∠APF=∠BAP,

同理∠CPF=∠DCP.

又因为∠APC=∠APF-∠CPF,

所以∠BAP-∠DCP=∠APC.