��Ŀ����
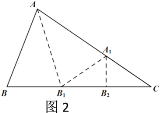
����Ŀ����ͼ1����ABC�У�����BAC��ƽ����AB1�۵��������ص����֣������²�������B1A1C��ƽ����A1B2�۵��������ص����֣����������²�������BnAnC��ƽ����AnBn+1�۵�����Bn���C�غϣ������۵����ٴΣ�ֻҪ���һ��ǡ���غϣ����Ǿͳ���BAC����ABC�ĺý�.

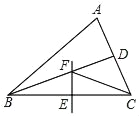
��1����ͼ2������ABC�У���B>��C�������������۵�����BAC����ABC�ĺýǣ�����B����C�ĵ�����ϵ��_______��
��2�����һ�������ε���С����20������������ε�����Ϊ______ʱ���������ε������Ǿ��Ǵ������εĺýǡ�
���𰸡�![]() 140����120����80��
140����120����80��
��������
��1�������۵����ʿɵá�A1B1B2=��C����AA1B1=��B����������������ʿɵá�AA1B1=2��C�����ݵ��������ɵá�B=2��C����2����������������۵�����BAC����ABC�ĺý�ʱ����B���C�ĵ�����ϵΪ��B=3��C�������ɵþ���n���۵�����BAC����ABC�ĺý�ʱ��B���C�ĵ�����ϵΪ��B=n��C����Ϊ��С����20������ABC�ĺýǣ����ݺýǶ��壬�������Ƿֱ�Ϊ20m��4mn�����������20m+20mn+20=180��������m(n+1)=8���ٸ���m��n�����������ɵ�m��n+1��8���������ӣ��Ӷ�������ý����
��1�������۵����ʵá�B=��AA1B1����A1B1B2=��C��
�ߡ�AA1B1=��A1B1B2+��C��
���B=2��C
�ʴ�Ϊ����B=2��C
��2����ͼ���߸����۵�������֪����B=��AA1B1����C=��A2B2C����A1B1C=��A1A2B2��
����������ε���Ƕ���֪����A1A2B2=��C+��A2B2C=2��C��
�߸����ı��ε���Ƕ���֪����BAC+��B+��AA1B1-��A1B1C=��BAC+2��B-2��C=180����
����������ABC���ڽǺͶ���֪����BAC+��B+��C=180����
���B=3��C��

�൱��B=2��Cʱ����BAC����ABC�ĺýǣ�����B=3��Cʱ����BAC����ABC�ĺýǣ�
��������n���۵���BAC����ABC�ĺýǣ����B���C���������B����C��֮��ĵ�����ϵΪ��B=n��C��
����С��Ϊ20����
������������Ϊ20m����20mn����
��20��+20m��+20mn��=180������m(1+n)=8��
��m��n������
��m=1��1+n=8����m=2��1+n=4����m=4��1+n=2.
��ã�m=1��n=7��m=2��n=3��m=4��n=1��
����������Ϊ20����140����40����120����80����80����
�������������Ϊ140����120����80��ʱ�������Ǿ��Ǵ������εĺý�.
�ʴ�Ϊ��140����120����80��

 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д�