题目内容
【题目】如图,矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上,线段OA、OC的长度满足方程|x﹣15|+ ![]() =0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD=
=0(OA>OC),直线y=kx+b分别与x轴、y轴交于M、N两点,将△BCN沿直线BN折叠,点C恰好落在直线MN上的点D处,且tan∠CBD= ![]()
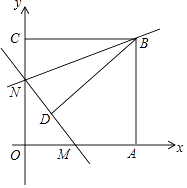
(1)求点B的坐标;
(2)求直线BN的解析式;
(3)将直线BN以每秒1个单位长度的速度沿y轴向下平移,求直线BN扫过矩形AOCB的面积S关于运动的时间t(0<t≤13)的函数关系式.
【答案】
(1)解:∵|x﹣15|+ ![]() =0,
=0,
∴x=15,y=13,
∴OA=BC=15,AB=OC=13,
∴B(15,13)
(2)解:如图1,过D作EF⊥OA于点E,交CB于点F,
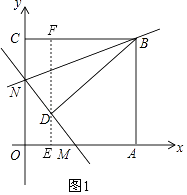
由折叠的性质可知BD=BC=15,∠BDN=∠BCN=90°,
∵tan∠CBD= ![]() ,
,
∴ ![]() =
= ![]() ,且BF2+DF2=BD2=152,解得BF=12,DF=9,
,且BF2+DF2=BD2=152,解得BF=12,DF=9,
∴CF=OE=15﹣12=3,DE=EF﹣DF=13﹣9=4,
∵∠CND+∠CBD=360°﹣90°﹣90°=180°,且∠ONM+∠CND=180°,
∴∠ONM=∠CBD,
∴ ![]() =
= ![]() ,
,
∵DE∥ON,
∴ ![]() =
= ![]() =
= ![]() ,且OE=3,
,且OE=3,
∴ ![]() =
= ![]() ,解得OM=6,
,解得OM=6,
∴ON=8,即N(0,8),
把N、B的坐标代入y=kx+b可得 ![]() ,解得
,解得 ![]() ,
,
∴直线BN的解析式为y= ![]() x+8
x+8
(3)解:设直线BN平移后交y轴于点N′,交AB于点B′,
当点N′在x轴上方,即0<t≤8时,如图2,
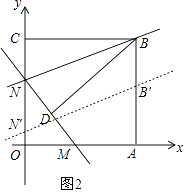
由题意可知四边形BNN′B′为平行四边形,且NN′=t,
∴S=NN′OA=15t;
当点N′在y轴负半轴上,即8<t≤13时,设直线B′N′交x轴于点G,如图3,
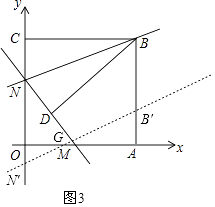
∵NN′=t,
∴可设直线B′N′解析式为y= ![]() x+8﹣t,
x+8﹣t,
令y=0,可得x=3t﹣24,
∴OG=24,
∵ON=8,NN′=t,
∴ON′=t﹣8,
∴S=S四边形BNN′B′﹣S△OGN′=15t﹣ ![]() (t﹣8)(3t﹣24)=﹣
(t﹣8)(3t﹣24)=﹣ ![]() t2+39t﹣96;
t2+39t﹣96;
综上可知S与t的函数关系式为S= 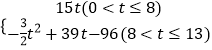
【解析】(1)由两个非负数的和为0,每个非负数均为0可得x=15,y=13,即B(15,13);(2)要利用三角函数tan∠CBD= ![]() ,就须过D作垂线,把∠CBD放在直角三角形中,再由平行线分线段成比例列出方程,求出OM=6,利用待定系数法求出直线BN的解析式;(3)须动手操作平移BN,可发现扫过的图形分为平行四边形和五边形两种,当NN′B′为平行四边形时面积利用底
,就须过D作垂线,把∠CBD放在直角三角形中,再由平行线分线段成比例列出方程,求出OM=6,利用待定系数法求出直线BN的解析式;(3)须动手操作平移BN,可发现扫过的图形分为平行四边形和五边形两种,当NN′B′为平行四边形时面积利用底![]() 高;当扫过面积为五边形时,用作差法S四边形BNN′B′﹣S△OGN′,用t 的代数式表示两部分面积即可.
高;当扫过面积为五边形时,用作差法S四边形BNN′B′﹣S△OGN′,用t 的代数式表示两部分面积即可.
【考点精析】认真审题,首先需要了解函数关系式(用来表示函数关系的数学式子叫做函数解析式或函数关系式).