题目内容
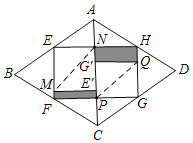
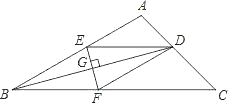
【题目】如图,在 ABC 中,BD 平分ABC 交 AC 于 D ,EF 垂直平分 BD ,分别交 AB, BC, BD于 E, F , G ,连接 DE, DF 。
(1)求证:四边形 BEDF 为菱形;
(2)若ABC 30, C 45, DE 4 ,求CF 的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)先根据垂直平分线的性质得:DE=BE,DF=FB,证明△BEG≌△BFG(ASA),根据对角线互相平分的四边形是平行四边形得:四边形DFBE是平行四边形,再由一组邻边相等的平行四边是菱形可得结论;
(2)过D作DH⊥CF于H.在Rt△DFH中,求出DH、FH,在Rt△DHC中,求出CH即可解决问题;
(1)证明:∵EF是BD的垂直平分线,
∴DE=EB,DF=BF,∠EGB=∠FGB=90°,DG=BG
∵BD平分∠ABC,
∴∠EBG=∠FBG,
∵BG=BG,
∴△BEG≌△BFG(ASA),
∴GE=GF,
∴四边形DFBE是平行四边形,
∵DE=BE,
∴四边形DFBE是菱形;
(2)解:过D作DH⊥CF于H.
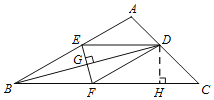
∵四边形BFDE是菱形,
∴DF∥AB,DE=DF=4.
在Rt△DFH中,∠DFC=∠ABC=30°,
![]()
在Rt△CDH中,∠C=45°,
∴DH=HC=2,
![]()

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目