题目内容
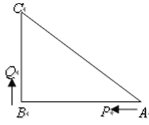
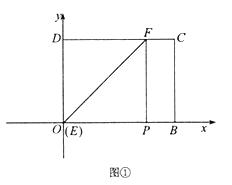
【题目】已知矩形纸片OBCD的边OB在x轴上,OD在y轴上,点C在第一象限,且![]() .现将纸片折叠,折痕为EF(点E,F是折痕与矩形的边的交点),点P为点D的对应点,再将纸片还原。
.现将纸片折叠,折痕为EF(点E,F是折痕与矩形的边的交点),点P为点D的对应点,再将纸片还原。
(I)若点P落在矩形OBCD的边OB上,
①如图①,当点E与点O重合时,求点F的坐标;
②如图②,当点E在OB上,点F在DC上时,EF与DP交于点G,若![]() ,求点F的坐标:
,求点F的坐标:
(Ⅱ)若点P落在矩形OBCD的内部,且点E,F分别在边OD,边DC上,当OP取最小值时,求点P的坐标(直接写出结果即可)。

【答案】(I)①点F的坐标为![]() ;②点F的坐标为
;②点F的坐标为![]() ;(II)
;(II)![]()
【解析】
(I)①根据折叠的性质可得![]() ,再由矩形的性质,即可求出F的坐标;
,再由矩形的性质,即可求出F的坐标;
②由折叠的性质及矩形的特点,易得![]() ,得到
,得到![]() ,再加上平行,可以得到四边形DEPF是平行四边形,在由对角线垂直,得出
,再加上平行,可以得到四边形DEPF是平行四边形,在由对角线垂直,得出 ![]() 是菱形,设菱形的边长为x,在
是菱形,设菱形的边长为x,在![]() 中,由勾股定理建立方程即可求解;
中,由勾股定理建立方程即可求解;
(Ⅱ)当O,P,F点共线时OP的长度最短.
解:(I)①∵折痕为EF,点P为点D的对应点
![]()
![]()
∵四边形OBCD是矩形,
![]()
![]()
![]()
点F的坐标为![]()
②∵折痕为EF,点P为点D的对应点.
![]()
∵四边形OBCD是矩形,
![]() ,
,
![]() ;
;
![]()
![]()
![]()
![]()
∴四边形DEPF是平行四边形.
![]() ,
,
![]() 是菱形.
是菱形.
设菱形的边长为x,则![]()
![]() ,
,
![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]()
![]()
解得![]()
![]()
∴点F的坐标为![]()
(Ⅱ)![]()

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
【题目】车间有20名工人,某一天他们生产的零件个数统计如下表:
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?