题目内容
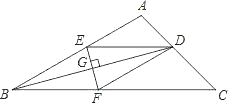
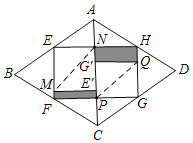
【题目】在关于“折纸问题”的数学活动课中，小刚沿菱形纸片ABCD各边中点的连线裁剪得到四边形纸片EFGH，再将纸片EFGH按如图所示分别沿MN、P2折叠，使点E，G落在线段PN上点E，G处，当PNEF时，若阴影部分的周长之和为16，△AEH，△CFG的面积之和为12，则菱形纸片ABCD的一条对角线BD的长为_____．
【答案】12
【解析】
证出EH是△ABD的中位线，得出BD＝2EH＝4HN，由题意可以设AN＝PC＝x，EN＝HN＝PF＝PG＝y．构建方程组求出x，y即可解决问题．
解：连接BD，如图所示：
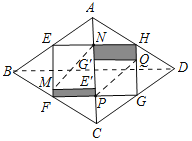
∵四边形ABCD是菱形，
∴AB＝AD，AC与BD垂直平分，
∵E是AB的中点，H是AD的中点，
∴AE＝AH，EH是△ABD的中位线，
∴EN＝HN，BD＝2EH＝4HN，
由题意可以设AN＝PC＝x，EN＝HN＝PF＝PG＝y．
则有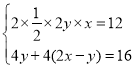
，
解得：
，
∴AN＝2，HN＝3，
∴BD＝4HN＝12；
故答案为：12
天天向上一本好卷系列答案
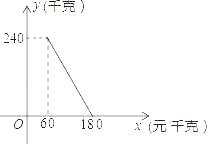
小学生10分钟应用题系列答案
【题目】瑞安市曹村镇“八百年灯会”成为温州“申遗”的宝贵项目．某公司生产了一种纪念花灯，每件纪念花灯制造成本为18元．设销售单价x（元），每日销售量y（件）每日的利润w（元）．在试销过程中，每日销售量y（件）、每日的利润w（元）与销售单价x（元）之间存在一定的关系，其几组对应量如下表所示：
（元） | 19 | 20 | 21 | 30 |
（件） | 62 | 60 | 58 | 40 |
（1）根据表中数据的规律，分别写出毎日销售量y（件），每日的利润w（元）关于销售单价x（元）之间的函数表达式．（利润＝（销售单价﹣成本单价）×销售件数）．
（2）当销售单价为多少元时，公司每日能够获得最大利润？最大利润是多少？
（3）根据物价局规定，这种纪念品的销售单价不得高于32元，如果公司要获得每日不低于350元的利润，那么制造这种纪念花灯每日的最低制造成本需要多少元？
