Question

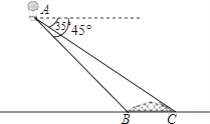
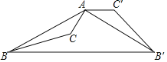
【题目】如图，以点A为中心，把△ABC逆时针旋转，得到△（点B、C的对应点分别为点、C’），连接，若∥，则∠的度数为　　

A. B. C. D.

Answer 1

【答案】D

【解析】

根据旋转的性质得到∠BAB′=∠CAC′=120°，AB=AB′，根据等腰三角形的性质易得∠AB′B=30°，再根据平行线的性质即可得∠C′AB′=∠AB′B=30°，从而可求∠CAB′．

解：∵将△ABC逆时针旋转120°得到△AB′C′，

∴∠BAB′=∠CAC′=120°，AB=AB′，

∴∠AB′B=(180°-120°)=30°，

∵AC′∥BB′，

∴∠C′AB′=∠AB′B=30°，

∴∠CAB′=∠CAC′-∠C′AB′=120°-30°=90°.

故选D.