题目内容
【题目】已知抛物线![]() .
.
(1)若该抛物线与x轴有公共点,求c的取值范围;
(Ⅱ)设该抛物线与直线![]() 交于M,N两点,若
交于M,N两点,若![]() ,求C的值;
,求C的值;
(Ⅲ)点P,点Q是抛物线上位于第一象限的不同两点,![]() 都垂直于x轴,垂足分别为A,B,若
都垂直于x轴,垂足分别为A,B,若![]() ,求c的取值范围.
,求c的取值范围.
【答案】(I)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)c的取值范围是
;(Ⅲ)c的取值范围是![]()
【解析】
(1) 抛物线与x轴有公共点,则判别式为非负数,列不等式求解即可;
(2)求出二次函数与直线的交点,并根据勾股定理求出MN的长度,列方程即可求解;
(3)由![]() 可知,P,Q两点的坐标特点,设坐标得到设点P的坐标为
可知,P,Q两点的坐标特点,设坐标得到设点P的坐标为![]() ,则点Q的坐标为
,则点Q的坐标为![]() ,代入二次函数,得到n,m的关系,则只需保证该方程有正根即可求解.
,代入二次函数,得到n,m的关系,则只需保证该方程有正根即可求解.
解:(I)∵抛物线![]() 与x轴有交点,
与x轴有交点,
∴一元二次方程![]() 有实根。
有实根。
![]() ,即
,即![]() .解得
.解得![]()
(Ⅱ)根据题意,设![]()
由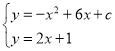 ,消去y,得
,消去y,得![]() ①.
①.
由![]() ,得
,得![]() .
.
∴方程①的解为![]()
![]()
![]() ,解得
,解得![]()
(Ⅲ)设点P的坐标为![]() ,则点Q的坐标为
,则点Q的坐标为![]() ,且
,且![]() ,
,
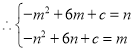 ,两式相减,得
,两式相减,得![]() ,即
,即![]()
![]() ,即
,即![]()
![]() ,其中
,其中![]()
由![]() ,即
,即![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,不合题意。
,不合题意。
又![]() ,得
,得![]() .
.
∴c的取值范围是![]()

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目