题目内容
已知：如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF。求证： EB∥DF （本题6分） 
连接BD,交AC于点O
∵ ABCD
∴AO=CO,BO=DO
∵AE=CF
∴EO=FO
∴四边形EBFD是平行四边形
∴EB∥DF
∵ ABCD∴AO=CO,BO=DO
∵AE=CF
∴EO=FO
∴四边形EBFD是平行四边形
∴EB∥DF
由四边形ABCD是平行四边形，根据平行四边形的对边平行且相等，可得AB∥CD，AB=CD，根据两直线平行，内错角相等，可得∠FCD=∠EAB，由已知AE=CF，可证得△FCD≌△EAB（SAS），所以EB=DF．
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
相关题目
为
边的中点，连结DE并延长DE交AB延长线于F. 求证：
．
，BE平分∠ABC且交CD于E，E为CD的中点，EF∥BC交AB于F，EG∥AB交BC于G，当
，
时，四边形BGEF的周长为 ．
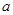，则阴影部分的面积为【 】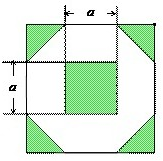
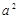
，试求
的度数（7分）
中，
，半径为1的动圆⊙
从
点出发，以每秒3个单位的速度沿折线
向终点
移动，设移动的时间为秒；同时，⊙
的半径
不断增大，且
(≥0).(1)当
秒时,两圆的位置关系是 ；(2)当t≥4秒时,若两圆外切,则t的值为 秒. 