题目内容
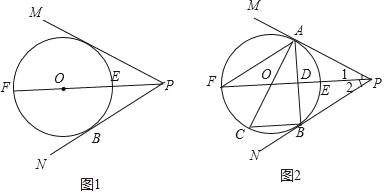
【题目】如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于点E,O是AB上一点,经过A,E两点的⊙O交AB于点D,连接DE,作∠DEA的平分线EF交⊙O于点F,连接AF.
(1)求证:BC是⊙O的切线;
(2)若sin∠EFA=![]() ,AF=
,AF=![]() ,求线段AC的长.
,求线段AC的长.

【答案】(1)证明见解析;(2)6.4.
【解析】
(1)连接OE,根据等腰三角形的性质和角平分线定义可得![]() ,根据平行线的判定可得OE∥AC,再由平行线的性质可得∠BEO=∠C=90°,即可证得结论;(2)连接
,根据平行线的判定可得OE∥AC,再由平行线的性质可得∠BEO=∠C=90°,即可证得结论;(2)连接![]() ,根据已知条件易证
,根据已知条件易证![]() .在
.在![]() 中,根据勾股定理求得
中,根据勾股定理求得![]() .根据同弧所对的圆周角相等及已知条件可得
.根据同弧所对的圆周角相等及已知条件可得![]() .在
.在![]() 中求得AE的长,再证明ΔACE∽ΔAED,根据相似三角形的性质即可求得线段AC的长.
中求得AE的长,再证明ΔACE∽ΔAED,根据相似三角形的性质即可求得线段AC的长.
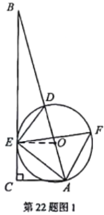
证明:(1)如图1,连接![]() ,
,
∵![]() ,
,
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() ∥
∥![]() ,
,
∴![]() .
.
∴![]()
∵![]() 为
为![]() 的半径,
的半径,
∴![]() 是
是![]() 的切线.
的切线.
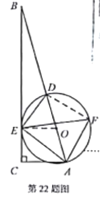
(2)如图2,连接![]() .
.
由题可知![]() 为
为![]() 的直径,
的直径,
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() .
.
∴![]() .
.
∴△AFD为等腰直角三角形,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ∽
∽![]() .
.
∴![]() .
.
∴![]() (或6.4)
(或6.4)

 名校课堂系列答案
名校课堂系列答案【题目】城南中学九年级共有12个班,每班48名学生,学校对该年级学生数学学科学业水平测试成绩进行了抽样分析,请按要求回答下列问题:
(1)(收集数据)要从九年级学生中抽取一个48人的样本,你认为以下抽样方法中最合理的是________.
①随机抽取一个班级的48名学生;②在九年级学生中随机抽取48名女学生;③在九年级12个班中每班各随机抽取4名学生.
(2)(整理数据)将抽取的48名学生的成绩进行分组,绘制成绩频数分布表和成绩分布扇形统计图如下.
请根据图表中数据填空:
①表中m的值为________;
② B类部分的圆心角度数为________°;
③估计C、D类学生大约一共有________名.

九年级学生数学成绩频数分布表
成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 24 |
|
B类(60~79) | 12 |
|
C类(40~59) | 8 | m |
D类(0~39) | 4 |
|
(3)(分析数据)教育主管部们为了解学校学生成绩情况,将同层次的城南、城北两所中学的抽样数据进行对比分析,得到下表:
学校 | 平均数(分) | 方差 | A、B类的频率和 |
城南中学 | 71 | 358 | 0.75 |
城北中学 | 71 | 588 | 0.82 |
请你评价这两所学校学生数学学业水平测试的成绩,提出一个解释来支持你的观点.