��Ŀ����
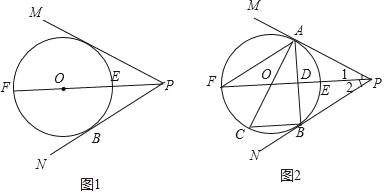
����Ŀ����ͼ1����֪��MPN�Ľ�ƽ����PF����Բ��O����O�ڵ�E��F��PN����O�����ߣ�BΪ�е㣮
��1����֤��PMҲ����O�����ߣ�
��2����ͼ2���ڣ�1����ǰ���£�������PM����O���е�ΪA������AB��PF�ڵ�D������AO����O�ڵ�C������BC��AF������PFAΪ�Ϧ���
����BC=6��tan�Ϧ�=![]() �����߶�AD�ij���
�����߶�AD�ij���
��С��̽��ͼ2֮���֣�EF2=mODOP��mΪ�����������������m����ֵ����֤����Ľ��ۣ�
���𰸡���1�������������2����4����4.
��������
��1������O��OA��PM������ΪA������OB���������ߵ����ʿɵó�OB�ǡ�O�İ뾶��OB��PN����PFƽ�֡�MPN���ý�ƽ���ߵ����ʿɵó�OA=OB��������֤��PMҲ�ǡ�O�����ߣ�
��2������PM��PN���ǡ�O�����߿ɵó�PA=PB�����õ��������ε����ߺ�һ�ɵó�OP��AB��AD=BD������������λ�ߵ����ʿɵó�OD=3�����O�İ뾶Ϊr����FD=r+3��AD=![]() ��r+3������Rt��AOD�У����ù��ɶ��������r��ֵ���������AD=
��r+3������Rt��AOD�У����ù��ɶ��������r��ֵ���������AD=![]() ��r+3���м������AD�ij��ȣ�
��r+3���м������AD�ij��ȣ�
���ɡ�OAP=��ODA=90�㡢��AOP=��DOA��֤����OAP�ס�ODA���������������ε����ʿɵó�OA2=ODOP�����EF=2OA��֤��EF2=4ODOP����m=4��
��1��֤������ͼ1�У�����O��OA��PM������ΪA������OB��
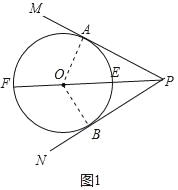
��PN����O�����ߣ�BΪ�е㣬
��OB����O�İ뾶����OB��PN��
��PFƽ����MPN��
��OA=OB��
��PMҲ����O�����ߣ�
��2���١�PM��PN������O�����ߣ�
��PA=PB��
�ߡ�APD=��BPD��
��OP��AB��AD=BD��
��ODΪ��ABC����λ�ߣ�
��OD=![]() BC=3��
BC=3��
����O�İ뾶Ϊr����FD=r+3��
��tan�Ϧ�=![]() ��
��
��AD=![]() ��r+3����
��r+3����
��Rt��AOD��OA2=AD2+OD2����r2=[![]() ��r+3��]2+32��
��r+3��]2+32��
��ã�r=5��
��AD=![]() ��r+3��=4��
��r+3��=4��
������m=4��
֤�����ߡ�OAP=��ODA=90�㣬��AOP=��DOA��
���OAP�ס�ODA��
��![]() ����OA2=ODOP��
����OA2=ODOP��
����EF=2OA��
��EF2=4ODOP��
��m=4��

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ���±���2018�����·�ij����С�������ȡ20���������ˮ�����
����ˮ��/�� | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
���� | 2 | 4 | m | 4 | 3 | 0 | 1 |
��1�����m=�� �������仭����20����ͥ���·��õ���������ͳ��ͼ��
��2�����ϱ����й���Ϣ��������ҳ��±��е�ͳ�������������������У�
ͳ�������� | ���� | ��λ�� | ƽ���� |
���� | �� �� | �� �� | �� �� |
��3��Ϊ�˳�������Լ��ˮ����ɫ����������ʶ������������ˮ��˾ʵ�����ݼ���ˮ������Ʒ������۸�����£�
����ˮ�ݼ��� | ������30�����ڣ� | ����������30�ֵIJ��֣� |
���ۣ�Ԫ/�֣� | 2.4 | 4 |
�����С����500����ͥ�������������ݣ�������С�����·��ж��ٻ���ͥ�ﵽ����������������Щ������ˮ������ˮ���Ƕ���Ԫ��



