题目内容
如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E, 延长BC到点F,使FC
=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中正确结论
的个数为( )
①OH=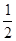 BF; ②∠CHF=45°; ③GH=
BF; ②∠CHF=45°; ③GH=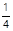 BC;④DH2=HE·HB
BC;④DH2=HE·HB
A. 1个 B. 2个 C. 3个 D. 4个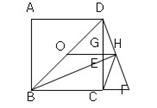
=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中正确结论
的个数为( )
①OH=
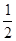 BF; ②∠CHF=45°; ③GH=
BF; ②∠CHF=45°; ③GH=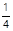 BC;④DH2=HE·HB
BC;④DH2=HE·HBA. 1个 B. 2个 C. 3个 D. 4个

C
作EJ⊥BD于J,连接EF

①∵BE平分∠DBC∴EC=EJ,∴△DJE≌△ECF∴DE=FE
∴∠HEF=45°+22.5°=67.5°∴∠HFE= =22.5°∴∠EHF=180°-67.5°-22.5°=90°
=22.5°∴∠EHF=180°-67.5°-22.5°=90°
∵DH=HF,OH是△DBF的中位线∴OH∥BF∴OH= BF
BF
②∵四边形ABCD是正方形,BE是∠DBC的平分线,∴BC=CD,∠BCD=∠DCF,∠EBC=22.5°,
∵CE=CF,∴Rt△BCE≌Rt△DCF,∴∠EBC=∠CDF=22.5°,
∴∠BFH=90°-∠CDF=90°-22.5°=67.5°,∵OH是△DBF的中位线,CD⊥AF,
∴OH是CD的垂直平分线,∴DH=CH,∴∠CDF=∠DCH=22.5°,
∴∠HCF=90°-∠DCH=90°-22.5°=67.5°,
∴∠CHF=180°-∠HCF-∠BFH=180°-67.5°-67.5°=45°,故②正确;
③∵OH是△BFD的中位线,∴DG=CG= BC,GH=
BC,GH= CF,∵CE=CF,∴GH=
CF,∵CE=CF,∴GH= CF=
CF= CE
CE
∵CE<CG= BC,∴GH<
BC,∴GH< BC,故此结论不成立;
BC,故此结论不成立;
④∵∠DBE=45°,BE是∠DBF的平分线,∴∠DBH=22.5°,由②知∠HBC=∠CDF=22.5°,
∴∠DBH=∠CDF,∵∠BHD=∠BHD,∴△DHE∽△BHD,∴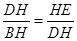 ∴DH=HE•HB,故④成立;
∴DH=HE•HB,故④成立;
所以①②④正确.故选C.

①∵BE平分∠DBC∴EC=EJ,∴△DJE≌△ECF∴DE=FE
∴∠HEF=45°+22.5°=67.5°∴∠HFE=
 =22.5°∴∠EHF=180°-67.5°-22.5°=90°
=22.5°∴∠EHF=180°-67.5°-22.5°=90°∵DH=HF,OH是△DBF的中位线∴OH∥BF∴OH=
 BF
BF②∵四边形ABCD是正方形,BE是∠DBC的平分线,∴BC=CD,∠BCD=∠DCF,∠EBC=22.5°,
∵CE=CF,∴Rt△BCE≌Rt△DCF,∴∠EBC=∠CDF=22.5°,
∴∠BFH=90°-∠CDF=90°-22.5°=67.5°,∵OH是△DBF的中位线,CD⊥AF,
∴OH是CD的垂直平分线,∴DH=CH,∴∠CDF=∠DCH=22.5°,
∴∠HCF=90°-∠DCH=90°-22.5°=67.5°,
∴∠CHF=180°-∠HCF-∠BFH=180°-67.5°-67.5°=45°,故②正确;
③∵OH是△BFD的中位线,∴DG=CG=
 BC,GH=
BC,GH= CF,∵CE=CF,∴GH=
CF,∵CE=CF,∴GH= CF=
CF= CE
CE∵CE<CG=
 BC,∴GH<
BC,∴GH< BC,故此结论不成立;
BC,故此结论不成立;④∵∠DBE=45°,BE是∠DBF的平分线,∴∠DBH=22.5°,由②知∠HBC=∠CDF=22.5°,
∴∠DBH=∠CDF,∵∠BHD=∠BHD,∴△DHE∽△BHD,∴
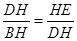 ∴DH=HE•HB,故④成立;
∴DH=HE•HB,故④成立;所以①②④正确.故选C.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目

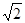 ,则另一直角边BC的长为 ▲ .
,则另一直角边BC的长为 ▲ .


 中,
中, 交
交 于
于 ,交
,交  的延长线于
的延长线于 ,若
,若 ,
, 厘米,则
厘米,则 厘米.
厘米.
 那么
那么 = (用
= (用 表示).
表示).