题目内容
如图，在正方形ABCD中，G是对角线AC上一点，GE⊥AB，GF⊥BC，垂足分别是E、F，连结EF、BG、DG。求证：DG=EF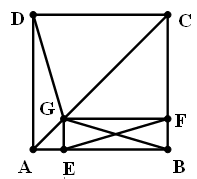
见解析
在正方形ABCD中，
∠ABC=∠BCD=Rt∠
CD=BC
AC平分∠BCD（正方形的性质）
∴∠ACD=∠ACB=45°---------2分
在△DCG和△BCG中
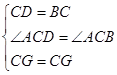
∴△DCG≌△BCG （SAS）
∴DG=BG-----------------------3分
∵GE⊥AB ，GF⊥BC
∴∠GEB=∠GFB=∠ABC =Rt∠
∴四边形BEGF是矩形（有三个角是直角的四边形是矩形）
∴EF=BG（矩形的对角线相等）--------------------------4分
∴DG=EF--------------------------1分
过点E作EN⊥AD于点N，作EM⊥CD于点M，证明△GEF≌△END，即可得出结论．
∠ABC=∠BCD=Rt∠
CD=BC
AC平分∠BCD（正方形的性质）
∴∠ACD=∠ACB=45°---------2分
在△DCG和△BCG中
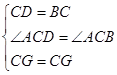
∴△DCG≌△BCG （SAS）
∴DG=BG-----------------------3分
∵GE⊥AB ，GF⊥BC
∴∠GEB=∠GFB=∠ABC =Rt∠
∴四边形BEGF是矩形（有三个角是直角的四边形是矩形）
∴EF=BG（矩形的对角线相等）--------------------------4分
∴DG=EF--------------------------1分
过点E作EN⊥AD于点N，作EM⊥CD于点M，证明△GEF≌△END，即可得出结论．
练习册系列答案
相关题目
为
边的中点，延长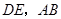
相交于点
．
．
，过
作
于
，
于
，则
的值为＿＿＿＿＿＿
中,AB∥
,
,以
、
、
为边向外作正方形
、
、
,面积为
、
、
，若
,当
时, 
______
,则
等于( ) 
那么
= （用
表示）．