题目内容
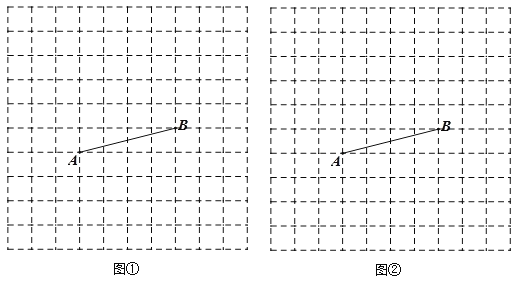
【题目】如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.
(1)求二次函数的解析式;
(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
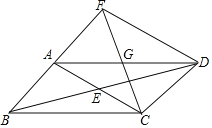
②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结EF,求△PEF周长的最小值.

【答案】(1)二次函数的解析式为:y=![]() x2+
x2+![]() x﹣6;
x﹣6;
(2)①P的运动路程为![]() ;②∠EPF的大小不会改变,理由见解析;
;②∠EPF的大小不会改变,理由见解析;
(3)C△PEF最小值为![]() .
.
【解析】试题分析:(1)由![]() 与
与![]() 轴分别交于A、B两点,且一元二次方程
轴分别交于A、B两点,且一元二次方程![]() 的两根为-8、2,可得点A、点B的坐标,即可得到OB的长,又由tan∠ABC=3,得到点C(0,-6),将 A、B、C的坐标代入二次函数中,即可得到二次函数解析式;
的两根为-8、2,可得点A、点B的坐标,即可得到OB的长,又由tan∠ABC=3,得到点C(0,-6),将 A、B、C的坐标代入二次函数中,即可得到二次函数解析式;
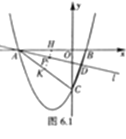
(2)①如图6.1,当l在AB位置时,P即为AB的中点H,当l运动到AC位置时,P即为AC的中点K,故P的运动路程为△ABC的中位线HK,在Rt△BOC中,由勾股定理得到BC的长,再由三角形中位线定理可得到HK的长,即P的运动路程;
②∠EPF的大小不会改变.由于,P为Rt△AED斜边AD的中点,故PE=![]() AD=PA,从而∠PAE=∠PEA=
AD=PA,从而∠PAE=∠PEA=![]() ∠EPD,同理有∠PAF=∠PFA=
∠EPD,同理有∠PAF=∠PFA=![]() ∠DPF,即可得到∠EPF=2∠EAF,故∠EPF的大小不会改变;
∠DPF,即可得到∠EPF=2∠EAF,故∠EPF的大小不会改变;
(3)设△PEF的周长为C,则![]() =PE+PF+EF=AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,得到∠EPG=
=PE+PF+EF=AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,得到∠EPG=![]() ∠EPF=∠BAC,由于tan∠BAC=
∠EPF=∠BAC,由于tan∠BAC=![]() ,故tan∠EPG=
,故tan∠EPG=![]() ,得到EG=
,得到EG=![]() PE,EF=
PE,EF=![]() PE=
PE=![]() AD,从而有
AD,从而有![]() =AD+EF=
=AD+EF=![]() AD=
AD=![]() AD,又当AD⊥BC时,AD最小,此时
AD,又当AD⊥BC时,AD最小,此时![]() 最小,由
最小,由![]() =30,得到AD=
=30,得到AD=![]() ,从而得到
,从而得到![]() 最小值.
最小值.
试题解析:(1)∵函数![]() 的图象与
的图象与![]() 轴分别交于A、B两点,且一元二次方程
轴分别交于A、B两点,且一元二次方程![]() 的两根为-8、2,∴A(-8,0)、B(2,0),即OB=2,又∵tan∠ABC=3,∴OC=6,即C(0,-6),将 A(-8,0)、B(2,0)代入
的两根为-8、2,∴A(-8,0)、B(2,0),即OB=2,又∵tan∠ABC=3,∴OC=6,即C(0,-6),将 A(-8,0)、B(2,0)代入![]() 中,解得:
中,解得: ![]() ,
, ![]() ,∴二次函数解析式为:
,∴二次函数解析式为: ![]() ;
;
(2)①如图6.1,当l在AB位置时,P即为AB的中点H,当l运动到AC位置时,P即为AC的中点K,∴P的运动路程为△ABC的中位线HK,∴HK=![]() BC,在Rt△BOC中,OB=2,OC=6,∴BC=
BC,在Rt△BOC中,OB=2,OC=6,∴BC=![]() ,∴HK=
,∴HK=![]() ,即P的运动路程为
,即P的运动路程为![]() ;
;
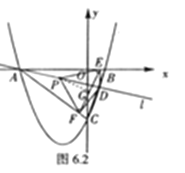
②∠EPF的大小不会改变.理由如下:
∵DE⊥AB,∴在Rt△AED中,P为斜边AD的中点,∴PE=![]() AD=PA,∴∠PAE=∠PEA=
AD=PA,∴∠PAE=∠PEA=![]() ∠EPD,同理可得:∠PAF=∠PFA=
∠EPD,同理可得:∠PAF=∠PFA=![]() ∠DPF,∴∠EPF=∠EPD+∠FPD=2(∠PAE+∠PAF),即∠EPF=2∠EAF,又∵∠EAF大小不变,∴∠EPF的大小不会改变;
∠DPF,∴∠EPF=∠EPD+∠FPD=2(∠PAE+∠PAF),即∠EPF=2∠EAF,又∵∠EAF大小不变,∴∠EPF的大小不会改变;
(3)设△PEF的周长为C,则![]() =PE+PF+EF,∵PE=
=PE+PF+EF,∵PE=![]() AD,PF=
AD,PF=![]() AD,∴
AD,∴![]() =AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,∴∠EPG=
=AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,∴∠EPG=![]() ∠EPF=∠BAC,∵tan∠BAC=
∠EPF=∠BAC,∵tan∠BAC=![]() ,∴tan∠EPG=
,∴tan∠EPG=![]() ,∴EG=
,∴EG=![]() PE,EF=
PE,EF=![]() PE=
PE=![]() AD,∴
AD,∴![]() =AD+EF=
=AD+EF=![]() AD=
AD=![]() AD,又当AD⊥BC时,AD最小,此时
AD,又当AD⊥BC时,AD最小,此时![]() 最小,∵
最小,∵![]() =30,∴
=30,∴![]() BC·AD=30,∴AD=
BC·AD=30,∴AD=![]() ,∴
,∴![]() 最小值为:
最小值为: ![]() AD=
AD=![]() .
.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案