��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l1��k1x+b�뷴��������![]() ��ͼ����A��B���㣨��A�ڵ�B��ࣩ����֪��A�������ǣ�6��2����B���������ǩ�3��
��ͼ����A��B���㣨��A�ڵ�B��ࣩ����֪��A�������ǣ�6��2����B���������ǩ�3��
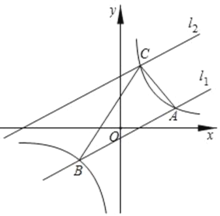
��1������������ֱ��l1�ı���ʽ��
��2������ͼ��ֱ��д��k1x+b��![]() �Ľ⼯��
�Ľ⼯��
��3����ֱ��l1��![]() ��y������ƽ�ƺ��ֱ��l2�뷴��������
��y������ƽ�ƺ��ֱ��l2�뷴��������![]() �ڵ�һ�����ڽ��ڵ�C�������ABC�����Ϊ30����ƽ�ƺ��ֱ��l2�ĺ�������ʽ��
�ڵ�һ�����ڽ��ڵ�C�������ABC�����Ϊ30����ƽ�ƺ��ֱ��l2�ĺ�������ʽ��
���𰸡���1��y��![]() ��y��
��y��![]() x��1����2����4��x��0��x��6����3��y��
x��1����2����4��x��0��x��6����3��y��![]() x+5��
x+5��
��������
��1������A��6��2������![]() �����k2��12���õ������������ı���ʽ����y��3���룬���x���õ�B�����꣬�ٽ�A��B������������l1��k1x��b�����ô���ϵ�������ֱ��l1�ı���ʽ��
�����k2��12���õ������������ı���ʽ����y��3���룬���x���õ�B�����꣬�ٽ�A��B������������l1��k1x��b�����ô���ϵ�������ֱ��l1�ı���ʽ��
��2���ҳ�һ�κ������ڷ���������ͼ���Ϸ��IJ��ֶ�Ӧ���Ա���x��ȡֵ��Χ���ɣ�
��3����ֱ��l1��x�ύ�ڵ�E��ƽ�ƺ��ֱ��l2��x�ύ�ڵ�D������AD��BD������CD��AB�����ɵó���ABC��������ABD�������ȣ����D��10��0�������ɵó�ƽ�ƺ��ֱ��l2�ĺ�������ʽ��
��1��������������![]() ��ͼ�����A��6��2����
��ͼ�����A��6��2����
��k2��6��2��12��
�������������ı���ʽΪy��![]() ��
��
������������y��![]() ��ͼ�����B��B���������ǩ�3��
��ͼ�����B��B���������ǩ�3��
��y����3ʱ��x����4��
��B����4����3����
��ֱ��l1��k1x+b��A��B���㣬
��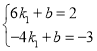 �����
����� ��
��
��ֱ��l1�ı���ʽΪy��![]() x��1��
x��1��
��2������ͼ��֪����4��x��0��x��6ʱ��һ�κ�����ͼ���ڷ���������ͼ����Ϸ���
����k1x+b��![]() �Ľ⼯Ϊ��4��x��0��x��6��
�Ľ⼯Ϊ��4��x��0��x��6��
��3����ͼ����ֱ��l1��x�ύ�ڵ�E��ƽ�ƺ��ֱ��l2��x�ύ�ڵ�D������AD��BD��
��CD��AB��
���ABC���������ABD�������ȣ�
�ߡ�ABC�����Ϊ30��
��S��ADE+S��BDE��30����![]() DE��|yA|+|yB|����30��
DE��|yA|+|yB|����30��
��![]() ��DE��5��30��
��DE��5��30��
��OD��12��
��E��
��D����10��0����
��ƽ�ƺ��ֱ��l2�ĺ�������ʽΪy��![]() x+n��
x+n��
��D����10��0�����룬�ɵ�0��![]() ������10��+n��
������10��+n��
���n��5��
��ƽ�ƺ��ֱ��l2�ĺ�������ʽΪy��![]() x+5��
x+5��