��Ŀ����
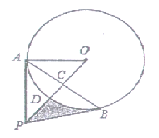
����Ŀ����ͼ�٣����壺ֱ��![]() ��x��y��ֱ��ཻ��A��B���㣬��
��x��y��ֱ��ཻ��A��B���㣬��![]() ���ŵ�O��ʱ����ת90��õ�
���ŵ�O��ʱ����ת90��õ�![]() ������A��B��D��������P����ֱ��
������A��B��D��������P����ֱ��![]() �ġ����������ߡ�����֮��ֱ��
�ġ����������ߡ�����֮��ֱ��![]() ����P�ġ�����ֱ��"�����ߡ���Ϊ�����ߡ���
����P�ġ�����ֱ��"�����ߡ���Ϊ�����ߡ���
��1����![]() �����������P�ĺ�������ʽ��____________��
�����������P�ĺ�������ʽ��____________��
��2���жϲ�˵��![]() ��
��![]() �Ƿ�Ϊ�����ߡ���
�Ƿ�Ϊ�����ߡ���
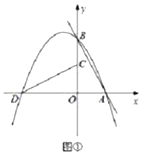
��3����ͼ�ڣ�������ֱ��![]() ������������P�ĶԳ�����
������������P�ĶԳ�����![]() �ཻ�ڵ�E����F��
�ཻ�ڵ�E����F��![]() �ϣ���Q��P�ĶԳ����ϣ����Ե�C��E��Q��FΪ������ı�������
�ϣ���Q��P�ĶԳ����ϣ����Ե�C��E��Q��FΪ������ı�������![]() Ϊһ�ߵ�ƽ���ı���ʱ�����Q�����꣮
Ϊһ�ߵ�ƽ���ı���ʱ�����Q�����꣮
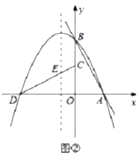
���𰸡��𰸼�����.
��������
��1����l��y=-2x+2�����A��B��C��D������ֱ�Ϊ����1��0������0��2������0��1������-2��0�����������ߵı���ʽΪ��y=a��x+2����x-1����������⣻
��2��ͬ������A��B��C��D������ֱ�Ϊ����k��0������0��2k������0��k������-2k��0�����������ߵı���ʽΪ��y=a��x+2k����x-k����������⣻
��3���Ե�C��E��Q��FΪ������ı�������CEΪһ�ߵ�ƽ���ı���ʱ��������ã�|xQ-xF|=1������m+1=��1��������⣮
�⣺��1����l��y=-2x+2�����A��B��C��D������ֱ�Ϊ����1��0������0��2������0��1������-2��0����
�������ߵı���ʽΪ��y=a��x+2����x-1����
����B�����������ʽ�ã�2=a��0+2����0-1������ã�a=-1��
�ʴ�Ϊ��y=-x2-x+2��
(2)ͬ������A��B��C��D������ֱ�Ϊ����k��0������0��2k������0��k������-2k��0����
�������ߵı���ʽΪ��y=a��x+2k����x-k����
����B�����������ʽ����ã�a=![]() ��
��
�������ߵı���ʽΪ��y=![]()
��y=-2x+2k��y��![]() ��������������
��������������
��A��B��C��D������ֱ�Ϊ����2��0������0��4������0��2������-4��0����
ͬ���ɵã������ߵı���ʽΪ��y=![]()
�����ߵĶԳ���Ϊ��x=-1��
���F��m��-2m+4������Q��-1��n����
����C��D���������һ�κ�������ʽ����ã�
ֱ��CD�ı���ʽΪ��y=![]() x+2��
x+2��
��CE�������Ϊ1�����������Ϊ![]() ��
��
�Ե�C��E��Q��FΪ������ı�������CEΪһ�ߵ�ƽ���ı���ʱ��
������ã�|xQ-xF|=1������m+1=��1��
��ã�m=0��-2��
��m=0ʱ����F��0��4�������Q��-1��![]() ����
����
ͬ����m=-2ʱ����Q��-1��![]() ����
����
���ϣ���Q����Ϊ��Q��-1��![]() ����Q��-1��
����Q��-1��![]() ����
����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�