题目内容
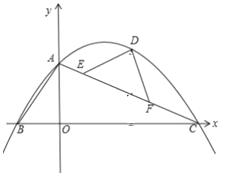
【题目】如图,平面直角坐标系中,O为坐标原点,直线y=﹣![]() x+4交x轴于点C,交y轴于点A,过A、C两点的抛物线y=ax2+bx+4交x轴负半轴于点B,且tan∠BAO=
x+4交x轴于点C,交y轴于点A,过A、C两点的抛物线y=ax2+bx+4交x轴负半轴于点B,且tan∠BAO=![]() .
.
(1)求抛物线的解析式;
(2)已知E、F是线段AC上异于A、C的两个点,且AE<AF,EF=2![]() ,D为抛物线上第一象限内一点,且DE=DF,设点D的横坐标为m,△DEF的面积为S,求S与m的函数关系式(不要求写出自变量m的取值范围);
,D为抛物线上第一象限内一点,且DE=DF,设点D的横坐标为m,△DEF的面积为S,求S与m的函数关系式(不要求写出自变量m的取值范围);
(3)在(2)的条件下,当∠EDF=90°时,连接BD,P为抛物线上一动点,过P作PQ⊥BD交线段BD于点Q,连接EQ.设点P的横坐标为t,求t为何值时,PE=QE.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)S=﹣
x+4;(2)S=﹣![]() m2+
m2+![]() m;(3)当t的值为1+
m;(3)当t的值为1+![]() 或1﹣
或1﹣![]() 时,PE=QE.
时,PE=QE.
【解析】
(1)令﹣![]() x+4=0,解得x=8,令x=0,y=4,由tan∠BAO=
x+4=0,解得x=8,令x=0,y=4,由tan∠BAO=![]() ,OA=4,得OB=3,由以上可得点A、B、C坐标,然后利用待定系数法进行求解即可;
,OA=4,得OB=3,由以上可得点A、B、C坐标,然后利用待定系数法进行求解即可;
(2)点坐标转换为线段长度,再利用相似三角形找到线段间的比例关系,继而可求出S与m的函数关系式;
(3)可利用(2)得到线段的长度,再综合分析(3)给出的已知信息,可知△EDF为等腰直角三角形,从而得到点E、D的坐标,继而结合三角形中位线定理等知识列式求解即可.
(1)令﹣![]() x+4=0,解得x=8,∴C(8,0),
x+4=0,解得x=8,∴C(8,0),
令x=0,y=4,∴A(0,4),AC=4![]() ,
,
∵tan∠BAO=![]() ,OA=4,∴OB=3,
,OA=4,∴OB=3,
∴B(﹣3,0),
将点B、C代入抛物线y=ax2+bx+4得,
![]() ,
,
解得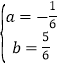 ,
,
∴抛物线得解析式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)如图所示,过点D作x轴的垂线,垂足为G,交AC于点K,过点D作EF的垂线,垂足为H,
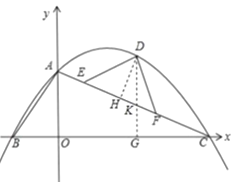
∵点D的横坐标为m,当x=m时,
y=﹣![]() m2+
m2+![]() m+4,
m+4,
设直线AC的解析式为y=kx+b,代入点A、C,
![]() ,
,
解得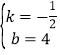 ,
,
∴y=﹣![]() x+4,
x+4,
∴K(m,﹣![]() m+4),
m+4),
∴DK=﹣![]() m2+
m2+![]() m+4﹣(﹣
m+4﹣(﹣![]() m+4)=﹣
m+4)=﹣![]() m2+
m2+![]() m,
m,
∵△DHK∽△COA,
∴![]() ,
,
∴![]() ,
,
∴DH=![]() (﹣
(﹣![]() m2+
m2+![]() m),
m),
∴S=![]() EFDH=﹣
EFDH=﹣![]() m2+
m2+![]() m;
m;
(3)由(2)可知,DH=![]() (﹣
(﹣![]() m2+
m2+![]() m),
m),
∵EF=2![]() ,DE=DF,且∠EDF=90°,
,DE=DF,且∠EDF=90°,
∴DH=![]() ,
,
∴![]() =
=![]() (﹣
(﹣![]() m2+
m2+![]() m),
m),
解得m1=3,m2=5,
当m=3时,点E与点A重合,不符合题意舍,
∴m=5,
∴D(5,4),
设点E的坐标为(k,﹣![]() k+4),DE=
k+4),DE=![]() EF=
EF=![]() ,
,
DE=![]() =
=![]() ,
,
解得k1=2,k2=6,
∵E在点D左侧,∴k=2,
∴E(2,3),
连接BD,设BD的解析式为y=kx+b,代入点B、D,
![]() ,解得
,解得![]() ,
,
∴直线BD的解析式为y=![]() x+
x+![]() ,
,
过点E作y轴的平行线交BD于点N,
则点N的坐标为(2,![]() ),
),
∴EN=![]() ,
,
连接PE并延长交BD于点K,
∵∠PQK=90°,EP=EQ,
∴∠EPQ=∠EQP,
∴∠EKQ=∠EQK,
∴EQ=EK=EP,
∴点E为PK的中点,
过点P作y轴的平行线交BD于点S,
∴PS=2EN,
∵P(t,-![]() t2+
t2+![]() t+4),
t+4),
∴S(t,![]() t+
t+![]() ),
),
∴PS=-![]() t2+
t2+![]() t+
t+![]() ,
,
∴-![]() t2+
t2+![]() t+
t+![]() =1,
=1,
解得t1=1+![]() ,t2=1﹣
,t2=1﹣![]() ,
,
∴当t的值为1+![]() 或1﹣
或1﹣![]() 时,PE=QE.
时,PE=QE.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案