题目内容
【题目】小明在一次数学兴趣小组活动中，进行了如下探索活动．
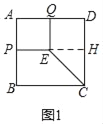
问题原型：如图（1），在矩形ABCD中，AB＝6，AD＝8，P、Q分别是AB、AD边的中点，以AP、AQ为邻边作矩形APEQ，连接CE，则CE的长为 （直接填空）
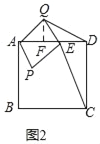
问题变式：（1）如图（2），小明让矩形APEQ绕着点A逆时针旋转至点E恰好落在AD上，连接CE、DQ，请帮助小明求出CE和DQ的长，并求DQ：CE的值．
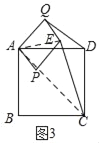
（2）如图（3），当矩形APEQ绕着点A逆时针旋转至如图（3）位置时，请帮助小明判断DQ：CE的值是否发生变化？若不变，说明理由．若改变，求出新的比值．
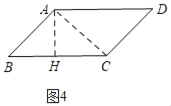
问题拓展：若将“问题原型”中的矩形ABCD改变为平行四边形ABCD，且AB＝3
，AD＝7，∠B＝45°，P、Q分别是AB、AD边上的点，且AP＝
AB，AQ＝AD，以AP、AQ为邻边作平行四边形APEQ．当平行四边形APEQ绕着点A逆时针旋转至如图（4）位置时，连接CE、DQ．请帮助小明求出DQ：CE的值．
【答案】问题原型：（1）CE＝5；问题变式：（1）CE＝3
，DQ＝
，DQ：CE＝4：5；（2）不变，见解析；问题拓展：
＝
【解析】
问题原型：如图1中，延长PE交CD于H，则四边形QEHD是矩形．在Rt△CEH中，利用勾股定理即可解决问题；
问题变式：（1）如图2中，作FQ⊥AD于F．利用勾股定理相似三角形的性质，分别求出CE、DQ即可解决问题；
（2）不变．理由如下：连接AE、AC．只要证明△ACE∽△ADQ，列比例式即可解决问题；
问题拓展：在图4中，计算AC的长，同理得△ACE∽△ADQ，通过计算即可解决问题．
问题原型：
如图1中，延长PE交CD于H，则四边形QEHD是矩形，
在Rt△CEH中，EH＝DQ＝4，CH＝PB＝AP＝3，
∴CE＝
＝5，
故答案为：5；
问题变式：
（1）如图2中，过Q作QF⊥AD于F，
在矩形APEQ中，∵AP＝3，EP＝4，
∴AE＝5，ED＝8﹣5＝3，
在Rt△CED中，CE＝
＝3，
∵∠QAF＝∠QAE，∠AFQ＝∠AQE＝90°，
∴△AQF∽△AEQ，
∴
，
∴
，
∴FQ＝
，
∴AF＝
，
∴DF＝8﹣
=
，
由勾股定理得：DQ＝
，
∴DQ：CE＝：3＝4：5；
（2）不变，理由如下：连接AE、AC，
由旋转可知：∠QAD＝∠EAC，
由勾股定理可知：AC＝10，AE＝5，
∴
，
，
∴
，
∴△ACE∽△ADQ，
∴
；
问题拓展：如图4中，过A作AH⊥BC于H，连接AC，
∵∠B＝45°，
∴△ABH是等腰直角三角形，
∵AB＝3
，
∴AH＝BH＝3
∴CH＝7﹣3＝4，
由勾股定理得：AC＝
＝5，
∴
，
如图5，连接AE、AC，
同理APEQ中，AP＝
，PE＝
，得AE＝
，
∴
，
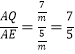由旋转得：∠QAD＝∠EAC，
∴△ACE∽△ADQ，可得：
．
