��Ŀ����
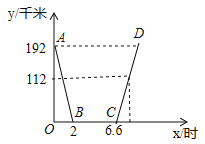
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У����κ���y=�� ![]() +bx+c��ͼ����A��1��0�����ҵ�x=0��x=5ʱ����Ӧ�ĺ���ֵ��ȣ�һ�κ���y=��x+3����κ���y=��
+bx+c��ͼ����A��1��0�����ҵ�x=0��x=5ʱ����Ӧ�ĺ���ֵ��ȣ�һ�κ���y=��x+3����κ���y=�� ![]() +bx+c��ͼ��ֱ���B��C���㣬��B�ڵ�һ���ޣ�
+bx+c��ͼ��ֱ���B��C���㣬��B�ڵ�һ���ޣ�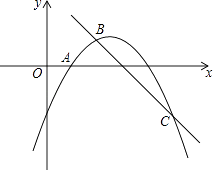
��1������κ���y=�� ![]() +bx+c�ı���ʽ��
+bx+c�ı���ʽ��
��2������AB����AB�ij���
��3������AC��M���߶�AC���е㣬����B�Ƶ�M��ת180��õ���N������AN��CN���ж��ı���ABCN����״����֤����Ľ��ۣ�
���𰸡�
��1��
�⣺��x=0ʱ��y=c������0��c����
�ɵ�x=0��x=5ʱ����Ӧ�ĺ���ֵ��ȣ��ã�5��c����
����5��c����1��0�����뺯������ʽ����
 ��
��
��� 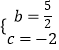 ��
��
�������ߵĽ���ʽΪy=�� ![]() x2+
x2+ ![]() x��2
x��2
��2��
�⣺������������ֱ�ߣ���
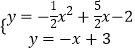 ��
��
��� ![]() ��
�� ![]() ��
��
��B��2��1����C��5����2����
�ɹ��ɶ�������
AB= ![]() =
= ![]()
��3��
�⣺��ͼ��
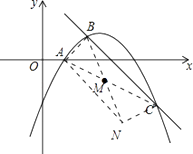 ��
��
�ı���ABCN��ƽ���ı��Σ�
֤������M��AC���е㣬
��AM=CM��
�ߵ�B�Ƶ�M��ת180��õ���N��
��BM=MN��
���ı���ABCN��ƽ���ı���
����������1�����ݵ�x=0��x=5ʱ����Ӧ�ĺ���ֵ��ȣ��ɵã�5��c�������ݴ���ϵ�������ɵú�������ʽ����2��������������ֱ�ߣ��ɵ÷����飬���ݽⷽ���飬�ɵ�B��C�����꣬���ݹ��ɶ������ɵ�AB�ij�����3�������߶��е�����ʣ��ɵ�M������꣬������ת�����ʣ��ɵ�MN��BM�Ĺ�ϵ������ƽ���ı��ε��ж����ɵô𰸣�
�����㾫����ͨ��������ö��κ�����ͼ��Ͷ��κ��������ʣ����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С�����Խ����⣮

 �Ͻ�ƽСѧ��������ϵ�д�
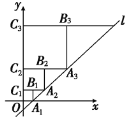
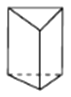
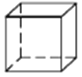
�Ͻ�ƽСѧ��������ϵ�д�����Ŀ���۲����ж����壬�����±���������.
���� | ������ | ������ | ������ | ������ |
ͼ�� |
|
|
|
|
������ | 6 | 10 | 12 | |
���� | 9 | 12 | ||
���� | 5 | 8 |
�۲��ϱ��еĽ�������ܷ���![]() ��
��![]() ��
��![]() ֮����ʲô��ϵ����д����ϵʽ
֮����ʲô��ϵ����д����ϵʽ