题目内容
【题目】如图,AB∥CD,CF平分∠ECD,HC⊥CF交直线AB于H,AG平分∠HAE交HC于G,EJ∥AG交CF于J,∠AEC=80°,则下列结论正确的有( )个.
①∠BAE+∠ECD=80°;②CG平分∠ICE;③∠AGC=140°;④∠EJC﹣∠AGH=90°.

A.1B.2C.3D.4
【答案】D
【解析】
作ET∥BH,如图1,由平行公理的推论可得ET∥CD,然后利用平行线的性质和角的和差即可判断①;
由垂直的定义可得∠ECH+∠ECF=90°,然后根据平角的定义和角平分线的定义即可判断②;
同①的方法可得∠AGC=∠GAH+∠GCI,然后根据角平分线的定义和①的结论即可判断③;
延长HC交EJ的延长线于R,如图2,由平行线的性质可得∠AGH=∠R,然后根据三角形的外角性质和已知条件HC⊥CF即可判断④.
解:作ET∥BH,如图1,则∠BAE=∠AET,
∵DC∥BH,
∴ET∥CD,
∴∠ECD=∠CET,
∴∠AEC=∠AET+∠CET=∠BAE+∠ECD=80°,故①正确;
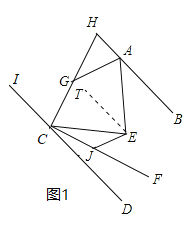
∵HC⊥CF,
∴∠ECH+∠ECF=90°,∠FCD+∠HCI=90°,
∵∠ECF=∠FCD,
∴∠ECH=∠HCI,
∴CH平分∠ECI,故②正确;
同①的方法可证:∠AGC=∠GAH+∠GCI=![]() (∠EAH+∠ECI)=
(∠EAH+∠ECI)=![]() (360°﹣∠BAE﹣∠ECD)=
(360°﹣∠BAE﹣∠ECD)=![]() (360°﹣80°)=140°,故③正确;
(360°﹣80°)=140°,故③正确;
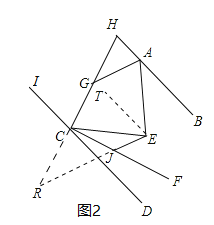
延长HC交EJ的延长线于R,如图2,
∵AG∥ER,
∴∠AGH=∠R,
∵∠EJC=∠R+∠RCJ,∠RCJ=90°,
∴∠EJC﹣∠AGH=90°,故④正确.
故选:D.

 阶梯计算系列答案
阶梯计算系列答案【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差 |
|
|
|
|
|
|
筐 数 |
|
|
|
|
|
|
(1)与标准质量比较,![]() 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价![]() 元,则出售这
元,则出售这![]() 筐白菜可卖多少元?
筐白菜可卖多少元?












