题目内容
【题目】如图,已知OM⊥ON,垂足为O,点A、B分别是射线OM、ON上的一点(O点除外).
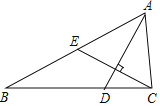
(1)如图①,射线AC平分∠OAB,是否存在点C,使得BC所在的直线也平分以B为顶点的某一个角α(0°<α<180°),若存在,则∠ACB= ;
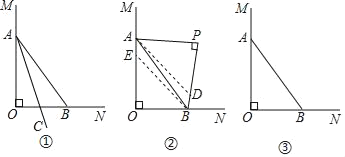
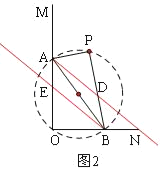
(2)如图②,P为平面上一点(O点除外),∠APB=90°,且OA≠AP,分别画∠OAP、∠OBP的平分线AD、BE,交BP、OA于点D、E,试简要说明AD∥BE的理由;
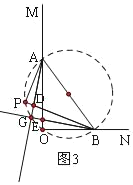
(3)在(2)的条件下,随着P点在平面内运动,AD、BE的位置关系是否发生变化?请利用图③画图探究,如果不变,直接回答;如果变化,画出图形并直接写出AD、BE位置关系.
【答案】(1)存在;45°或135°;(2)详见解析;(3)点P一直在以AB为直径的圆上,当P在直径AB的上方时,如图2,有AD∥BE,当P在直径AB的下方时,如图3,有AD⊥BE,
【解析】
(1)分两种情况讨论:①先根据垂直的定义可得:∠AOB=90°,再根据角平分线的定义得:∠ABC+∠BAC=![]() (∠ABO+∠BAO)=45°,由三角形内角和定理可得结论;②根据三角形外角的性质和角平分线的定义,可得结论;
(∠ABO+∠BAO)=45°,由三角形内角和定理可得结论;②根据三角形外角的性质和角平分线的定义,可得结论;
(2)证明∠OAD=∠OEB,可得:AD∥BE;
(3)先根据∠AOB=∠APB=90°,证明O、A、P、B四点共圆,即点P一直在以AB为直径的圆上,通过画图可知:当P在直径AB的上方时,如图2,有AD∥BE,当P在直径AB的下方时,如图3,有AD⊥BE.
解:(1)存在,
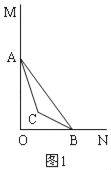
有两种情况:①当BC平分∠ABO时,如图1,
∵∠AOB=90°,
∴∠BAO+∠ABO=90°,
∵AC平分∠BAO,BC平分∠ABO,
∴∠BAC=![]() ,∠ABC=
,∠ABC=![]() ∠ABO,
∠ABO,
∴∠BAC+∠ABC=![]() (∠BAO+∠ABO)=45°,
(∠BAO+∠ABO)=45°,
∴∠ACB=180°﹣45°=135°;
②如下图,当CB平分∠ABN时,

∵∠ABN=90°+∠BAO,
∵AC平分∠BAO,
∴2∠ABE=90°+2∠CAB,
∴∠ABE=45°+∠CAB,
∴∠ACB=∠ABE﹣∠CAB=45°,
综上,∠ACB的度数为45°或135°;
故答案为:45°或135°;
(2)如图2,∵∠AOB=∠P=90°,
∴∠OAP+∠OBP=180°,
∴![]() ∠OAP+
∠OAP+![]() ∠OBP=90°,
∠OBP=90°,
∵AD平分∠OAP,BE平分∠OBP,
∴∠OAD=![]() ∠OAP=90°﹣
∠OAP=90°﹣![]() ,∠OBE=
,∠OBE=![]() ∠OBP,
∠OBP,
∵∠OBE+∠OEB=90°,
∴∠OEB=90°﹣∠OBE=90°﹣![]() ∠OBP,
∠OBP,
∴∠OAD=∠OEB,
∴AD∥BE;
(3)∵∠AOB=∠APB=90°,
∴点P一直在以AB为直径的圆上,
当P在直径AB的上方时,如图2,有AD∥BE,
当P在直径AB的下方时,如图3,有AD⊥BE,
理由是:∵∠OAP=∠OBP,
∵AD平分∠OAP,BE平分∠OBP,
∴∠PAD=![]() ∠OAP,∠DBE=
∠OAP,∠DBE=![]() ∠OBP,
∠OBP,
∴∠PAD=∠DBE,
∵∠ADP=∠BDG,
∴∠APB=∠AGB,
∴AD⊥BE.

 名校课堂系列答案
名校课堂系列答案