题目内容
【题目】阅读下面材料:
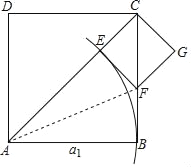
已知:如图,在正方形ABCD中,边AB=a1.
按照以下操作步骤,可以从该正方形开始,构造一系列的正方形,它们之间的边满足一定的关系,并且一个比一个小.
操作步骤 | 作法 | 由操作步骤推断(仅选取部分结论) |
第一步 | 在第一个正方形ABCD的对角线AC上截取AE=a1,再作EF⊥AC于点E,EF与边BC交于点F,记CE=a2 | (i)△EAF≌△BAF(判定依据是①); (ii)△CEF是等腰直角三角形; (iii)用含a1的式子表示a2为②: |
第二步 | 以CE为边构造第二个正方形CEFG; | |
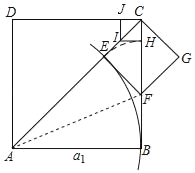
第三步 | 在第二个正方形的对角线CF上截取FH=a2,再作IH⊥CF于点H,IH与边CE交于点I,记CH=a3: | (iv)用只含a1的式子表示a3为③: |
第四步 | 以CH为边构造第三个正方形CHIJ | |
这个过程可以不断进行下去.若第n个正方形的边长为an,用只含a1的式子表示an为④ | ||
请解决以下问题:
(1)完成表格中的填空:
① ;② ;③ ;④ ;
(2)根据以上第三步、第四步的作法画出第三个正方形CHIJ(不要求尺规作图).
【答案】(1)①斜边和一条直角边分别相等的两个直角三角形全等②(![]() ﹣1)a1;③(
﹣1)a1;③(![]() -1)2a1;④(
-1)2a1;④(![]() -1)n-1a1;(2)见解析.
-1)n-1a1;(2)见解析.
【解析】
(1)①由题意可知在Rt△EAF和Rt△BAF中,AE=AB,AF=AF,所以Rt△EAF≌Rt△BAF;
②由题意得AB=AE=a1,AC=![]() a1,则CE=a2=
a1,则CE=a2=![]() a1﹣a1=(
a1﹣a1=(![]() ﹣1)a1;
﹣1)a1;
③同上可知CF=![]() CE=
CE=![]() (
(![]() -1)a1,FH=EF=a2,则CH=a3=CF﹣FH=(
-1)a1,FH=EF=a2,则CH=a3=CF﹣FH=(![]() -1)2a1;
-1)2a1;
④同理可得an=(![]() -1)n-1a1;
-1)n-1a1;
(2)根据题意画图即可.
解:(1)①斜边和一条直角边分别相等的两个直角三角形全等;
理由是:如图1,在Rt△EAF和Rt△BAF中,
∵![]() ,
,
∴Rt△EAF≌Rt△BAF(HL);
②∵四边形ABCD是正方形,
∴AB=BC=a1,∠ABC=90°,
∴AC=![]() a1,
a1,
∵AE=AB=a1,
∴CE=a2=![]() a1﹣a1=(
a1﹣a1=(![]() ﹣1)a1;
﹣1)a1;
③∵四边形CEFG是正方形,
∴△CEF是等腰直角三角形,
∴CF=![]() CE=
CE=![]() (
(![]() -1)a1,
-1)a1,
∵FH=EF=a2,
∴CH=a3=CF﹣FH=![]() (
(![]() -1)a1﹣(
-1)a1﹣(![]() -1)a1=(
-1)a1=(![]() -1)2a1;
-1)2a1;
④同理可得:an=(![]() -1)n-1a1;
-1)n-1a1;
故答案为:①斜边和一条直角边分别相等的两个直角三角形全等②(![]() ﹣1)a1;③(
﹣1)a1;③(![]() -1)2a1;④(
-1)2a1;④(![]() -1)n-1a1;
-1)n-1a1;
(2)所画正方形CHIJ见右图.

【题目】某中学开展“唱红歌”比赛活动,八年级1、2班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.

(1)根据统计图所给的信息填写下表;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
八(1) | 85 | _____ | 85 |
八(2) | _____ | 80 | _____ |
(2)若八(1)班复赛成绩的方差s12=70,请计算八(2)班复赛成绩的方差s22,并说明哪个班级5名选手的复赛成绩更平稳一些.








