题目内容
【题目】某市为了改善市区交通状况，计划在康富路的北端修建通往资江北岸的新大桥，如图，新大桥的两端位于A、B两点，小张为了测量A、B之间的河宽，在垂直于新大桥AB的直线型道路l上测得如下数据：∠BDA=76．1°，∠BCA=68．2°，CD=82米．求：AB的长（精确到0．1米，参考数据：sin76．1°≈0．97，cos76．1°≈0．24，tan76．1°≈4．0；sin68．2°≈0．93，cos68．2°≈0．37，tan68．2°≈2．5）．
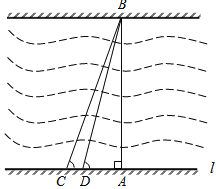
【答案】546．7米．
【解析】
试题设AD=x米，则AC=（x+82）米．在Rt△ABC中，根据三角函数得到AB=2.5（x+82），在Rt△ABD中，根据三角函数得到AB=4x，依此得到关于x的方程，进一步即可求解．
试题解析：设AD=x米，则AC=（x+82）米．
在Rt△ABC中，tan∠BCA=
，
∴AB=ACtan∠BCA=2.5（x+82）．
在Rt△ABD中，tan∠BDA=
，
∴AB=ADtan∠BDA=4x．
∴2.5（x+82）=4x，
解得：x=
，
∴AB=4x=4×≈546.7，
答：AB的长约为546.7米．
练习册系列答案
相关题目
