题目内容
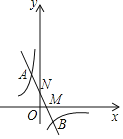
【题目】如图,关于x的一次函数y=k1x+b的图象与反比例函数y=![]() 的图象相交于A(﹣2,8),B(4,m)两点.
的图象相交于A(﹣2,8),B(4,m)两点.
(1)求一次函数与反比例函数的解析式.
(2)设一次函数y=k1x+b的图象与x轴,y轴的交点分别为M,N,P是x轴上一动点,当以P,M,N三点为顶点的三角形是等腰三角形时,求点P的坐标.
【答案】(1)y=﹣![]() ,y=﹣2x+4;(2)点P的坐标是(﹣2,0)或(2+2
,y=﹣2x+4;(2)点P的坐标是(﹣2,0)或(2+2![]() ,0)或(2﹣2
,0)或(2﹣2![]() ,0)或(﹣3,0).
,0)或(﹣3,0).
【解析】
(1)先把A点坐标代入y=![]() 可求出k2的值,从而确定反比例函数解析式;再把B(4,m)代入反比例函数解析式求出m的值,可确定点B的坐标,然后利用待定系数法求一次函数解析式;
可求出k2的值,从而确定反比例函数解析式;再把B(4,m)代入反比例函数解析式求出m的值,可确定点B的坐标,然后利用待定系数法求一次函数解析式;
(2)先根据一次函数的解析式确定M和N的坐标,根据以P,M,N三点为顶点的三角形是等腰三角形分三种情况讨论:①NP=NM;②MP=MN;③PN=PM;前两种直接根据线段的长得出点P的坐标,第三种根据两点的距离列方程可得结论.
解:(1)把![]() ,
,![]() 代入反比例函数
代入反比例函数![]() 得:
得:![]() ,
,
![]() ,
,![]() ,
,
∴反比例函数解析式为![]() ,且
,且![]() ,
,
把![]() ,
,![]() 代入
代入![]() 得:
得: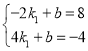 ,
,
解得![]() ,
,
∴一次函数解析式为![]() ;
;
(2)![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
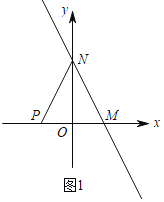
①当![]() 时,如图1,
时,如图1,
![]() ,
,
![]() ,
,
![]() ;
;
②当![]() 时,如图2,
时,如图2,
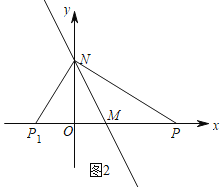
由勾股定理得:![]() ,
,
![]() ,
,![]() 或
或![]() ,
,![]() ;
;
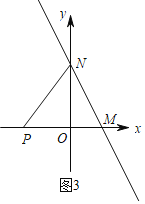
③当![]() 时,如图3,
时,如图3,
![]() 是
是![]() 轴上一动点,
轴上一动点,
![]() 设
设![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
综上,点![]() 的坐标是
的坐标是![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() .
.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目