äãá¢áÖàï
Àƒäãá¢À¢àÓë¥ùªòƒòúöØ¿º¿éǺ°úòÅÆûØåøë¤Õ£·ñø¤Õüçë°çáƒøý¢§ÄûÌåÙâÚë¥È˜ë¥øÅ![]() öˆüôùÛ¿Éçâ¢Öø݃ÑȘ
öˆüôùÛ¿Éçâ¢Öø݃ÑȘ![]() öˆ¢èàóæˆøÃ
öˆ¢èàóæˆøÃ![]() æåÆèæˆÑ₤çáñÏûéȘó§òÝñÏûéÝ£¿ÉçâøÅéé°—çáùÛ°Í¢ˆÈ˜¢èéé°—°úòÅöÜùÛȤçݤÆùÛèüíúòÝȘñÏûé£ÃØ·¤ÆùÛî¿óàѽ¿ÄÝíȘØåñâø¿¤ÆùÛç¿¿ÁàŠ°úøÅÈÛà¶ñÏûéçáø݃Ñ
æåÆèæˆÑ₤çáñÏûéȘó§òÝñÏûéÝ£¿ÉçâøÅéé°—çáùÛ°Í¢ˆÈ˜¢èéé°—°úòÅöÜùÛȤçݤÆùÛèüíúòÝȘñÏûé£ÃØ·¤ÆùÛî¿óàѽ¿ÄÝíȘØåñâø¿¤ÆùÛç¿¿ÁàŠ°úøÅÈÛà¶ñÏûéçáø݃Ñ![]() Ș
Ș![]() öˆ¥šÅßòÝñÏû颈ó¶çáö£øûȘúØ
öˆ¥šÅßòÝñÏû颈ó¶çáö£øûȘúØ![]() ÈÛ
ÈÛ
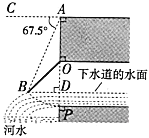
È´1ÈˋøݧÆÅÇ°—ñÏûéÝ£üôùÛçâçáùÛ°Í¢ˆÆŠÝ£¤ÆùÛ¿ÄÝí¿»°äøÅ![]() çáàÀøçñÑöÏÈ£
çáàÀøçñÑöÏÈ£
È´2Èˋöˆêù¿ÜýãùÛö£È˜çÝüôùÛçâçáùÛ°Í¢ˆñÏûéç§Çÿ![]() ö£øûòÝȘåÖçÐ
ö£øûòÝȘåÖçÐ![]() ÇÎýãçû¡ˋ§ú
ÇÎýãçû¡ˋ§ú![]() Șà¶ÇùòÝçÐ
Șà¶ÇùòÝçÐ![]() úÀ¤ûÆŠüôùÛçâçáùÛó§ûÌóŠó§È˜úµÇùòÝüôùÛçâáÖùÛçáèŸÑàÈÛÈ´§Ã¿«ÝÈ궡ª¤éÈˋ
úÀ¤ûÆŠüôùÛçâçáùÛó§ûÌóŠó§È˜úµÇùòÝüôùÛçâáÖùÛçáèŸÑàÈÛÈ´§Ã¿«ÝÈ궡ª¤éÈˋ
ÀƒÇÞ¯¡À¢È´1Èˋ![]() ȣȴ2Èˋ
ȣȴ2Èˋ![]()
Àƒ§ãö—À¢
(1)¡ªƒïäãØã¥Ç¢èçû秧ÃôÜÈ£
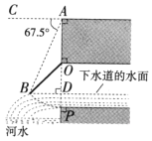
(2)¡ªƒïÆÁ§úçáÑ´ØÍçûç§ÀüBAO=22.5ÀÐȘ¡ªƒïçàî■໧úÅöçáÅåøòçûç§ÀüBAO=ÀüABO=22.5ÀÐȘÆè໧úÅöçáëã§úçáÅåøòçûç§ÀüBOP=45ÀÐȘ§ãøݧú໧úÅö¥Ç¢èçû秧ÃôÜÈÛ
§ãȤȴ1ÈˋñÏûé![]() Ý£üôùÛçâçáùÛ°Í¢ˆÆŠÝ£¤ÆùÛ¿ÄÝí¿»°äøÅȘ
Ý£üôùÛçâçáùÛ°Í¢ˆÆŠÝ£¤ÆùÛ¿ÄÝí¿»°äøÅȘ
![]() .
.
È´2ÈˋÀÔ![]() Ș
Ș![]() ȘÀÁ
ȘÀÁ![]()
ÀÔ![]() ȘÀÁ
ȘÀÁ![]() Ș
Ș
ÀÁ![]() .
.
àÓë¥È˜¿»çÐ![]() æ¼
æ¼![]() ÆÖçÐ
ÆÖçÐ![]() Ș
Ș
åÖ![]() øÅȘÀÔ
øÅȘÀÔ![]() Ș
Ș
ÀÁ![]() Ș
Ș
ÀÁ![]() .
.
ùªØåȘÇùòÝüôùÛçâáÖùÛçáèŸÑàå¥öˆ![]() .
.

Àƒäãá¢À¢á°øÅîϯùÀƒéꧡ—áõ¥Ñ¡¼ÆÅîÏèº180àùȘöˆêù§ãíãꧡ—áõ¥ÑîÏèºçáäÍøò§À¢çúÕ¢—Ș§½ÅÅêù°Õîªç¼ýÕȘ¿»°äàÓüôȤ
È´1Èˋòí¥₤ò»ƒï
ÇƯùÀƒéꧡ—áõ¥Ñ¡¼ùÌ£º°ÕàÀ20û«îÏèºÈ˜§½ÅÅêùäÍøò§À¢çýãòåȘýãòå°è¥´È´¯ìñøøóÈˋàÓüôȤ
¯ùáõ¥Ñ | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
ƒéáõ¥Ñ | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
È´2Èˋí«âÚÀÂûÒò—ò»ƒï
¯ÇàÓüôñøò»Ñöí«âÚÀÂûÒò—íãê§æÕîªÝƒò»ƒïȤ
°è¥´x | 40ÀÉxÀÉ49 | 50ÀÉxÀÉ59 | 60ÀÉxÀÉ69 | 70ÀÉxÀÉ79 | 80ÀÉxÀÉ89 | 90ÀÉxÀÉ100 |
¯ùáõ¥Ñ | 0 | 0 | 1 | 11 | 7 | 1 |
ƒéáõ¥Ñ | 1 | 0 | 0 | 7 | 10 | 2 |
È´ùçû¼È¤°è¥´80ñø¥¯ØåèüöˆäÍøò§À¢çÆéÅÐȘ70ˋ79ñøöˆäÍøò§À¢çꥤûȘ60ˋ69ñøöˆäÍøò§À¢ç¤ü¡þȘ60ñøØåüôöˆäÍøò§À¢çý£¤ü¡þÈˋ
È´3Èˋñøö—ò»ƒï
ê§æÕîªÝƒò»ƒïçá󧃪ò»ÀÂøÅö£ò»ÀÂøÖò»àÓüôÝÚȘúŠ§¨ÝÚ¡þý¿°ðëõí«È¤
󧃪ò» | øÅö£ò» | øÖò» | |
¯ùáõ¥Ñ | 78.3 | 77.5 | ÀÀ span>ÀÀ |
ƒéáõ¥Ñ | 78 | ÀÀ ÀÀ | 81 |
È´4Èˋçû°—§ÃôÜ
Âì¿â¥óƒéáõ¥Ñà¨äÍîÏèºøÅäÍøò§À¢çÆéÅÐçáîÏèºàùò»öˆÀÀ ÀÀ
ÂÖ¢èØåëóÑü°—ÀÀ ÀÀáõ¥ÑîÏèºçáäÍøò§À¢çúÕ¢—¡■¤ûØ£ÅˋȘâÚÆèöˆÀÀ ÀÀøêèìÇÆꧡ—ý£ë˜çá§úÑàùçû¼ëóÑüçá¤üâÚÅåÈˋ