ЬтФПФкШн
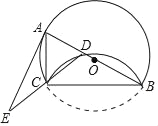
ЁОЬтФПЁПвбжЊЃКШчЭМЂйЃЌдкRtЁїABCжаЃЌЁЯABC=90ЁуЃЌBDЁЭACгкЕуDЃЌЧвAB=5ЃЌAD=4ЃЌдкADЩЯШЁвЛЕуGЃЌЪЙAG=![]() ЃЌЕуPЪЧелЯпCBЉBAЩЯвЛЖЏЕуЃЌвдPGЮЊжБОЖзїЁбOНЛACгкЕуEЃЌСЌНсPEЃЎ
ЃЌЕуPЪЧелЯпCBЉBAЩЯвЛЖЏЕуЃЌвдPGЮЊжБОЖзїЁбOНЛACгкЕуEЃЌСЌНсPEЃЎ
ЃЈ1ЃЉЧѓsinCЕФжЕЃЛ
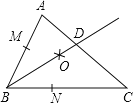
ЃЈ2ЃЉЕБЕуPгыЕуBжиКЯЪБШчЭМЂкЫљЪОЃЌЁбOНЛБпABгкЕуFЃЌЧѓжЄЃКЁЯEPG=ЁЯFPGЃЛ
ЃЈ3ЃЉЕуPдкећИідЫЖЏЙ§ГЬжаЃК
ЂйЕБBCЛђABгыЁбOЯрЧаЪБЃЌЧѓЫљгаТњзуЬѕМўЕФDEГЄЃЛ
ЂкЕуPвддВаФOЮЊа§зЊжааФЃЌЫГЪБеыЗНЯђа§зЊ90ЁуЕУЕНPЁфЃЌЕБPЁфЧЁКУТфдкABБпЩЯЪБЃЌЧѓЁїOPPЁфгыЁїOGEЕФУцЛ§жЎБШЃЈЧыжБНгаДГіД№АИЃЉЃЎ

ЁОД№АИЁПЃЈ1ЃЉsinЁЯC=![]() ЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉЂйDEГЄЮЊ
ЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉЂйDEГЄЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЛЂкТњзуЬѕМўЕФЁїOPPЁфгыЁїOGEЕФУцЛ§жЎБШЮЊ25ЃК24Лђ25ЃК7ЃЎ
ЃЛЂкТњзуЬѕМўЕФЁїOPPЁфгыЁїOGEЕФУцЛ§жЎБШЮЊ25ЃК24Лђ25ЃК7ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉвзжЄЁЯC=ЁЯABDЃЌдђsinЁЯC=sinЁЯABD=![]() =
=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉСЌНгCFЃЌИљОндВжмНЧЖЈРэЕУЁЯBFG=ЁЯAFG=90ЁуЃЌдђsinA=![]() ЃЌПЩЧѓЕУFG=
ЃЌПЩЧѓЕУFG=![]() ЃЌдйЧѓГіDG=ADЉAG=4Љ
ЃЌдйЧѓГіDG=ADЉAG=4Љ![]() =
=![]() ЃЌдђFG=DGЃЌМДПЩЕУжЄЃЛ
ЃЌдђFG=DGЃЌМДПЩЕУжЄЃЛ
ЃЈ3ЃЉЂйЁбOгыABЯрЧагаСНжжЧщПіЃЌгыBCЯрЧагавЛжжЧщПіЃЌШчЭМ3ЁЂ4ЁЂ5ЃЌСщЛюдЫгУЧаЯпЕФаджЪЃЌШ§НЧКЏЪ§гыЙДЙЩЖЈРэЗжБ№ЧѓНтМДПЩЃЛ
ЂкШчЭМ3жаЃЌгУЃЈ2ЃЉПЩжЊЃЌЕуPвддВаФOЮЊа§зЊжааФЃЌЫГЪБеыЗНЯђа§зЊ90ЁуЕУЕНPЃЌ
ЕБPЧЁКУТфдкABБпЩЯЪБЃЌДЫЪБЁїOPPЁфгыЁїOGEЕФУцЛ§жЎБШ=![]() ЁС
ЁС![]() ЁС
ЁС![]() ЃК
ЃК![]() ЁС
ЁС![]() ЁС
ЁС![]() ЁС
ЁС![]() =25ЃК24ЃЛ
=25ЃК24ЃЛ
ШчЭМ6жаЃЌЕБЁїPOHЪЧЕШбќжБНЧШ§НЧаЮЪБЃЌСЌНгPEЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪЧѓЕУAE=![]() ЃЌPE=
ЃЌPE=![]() ЃЌМДGE=AEЉAG=
ЃЌМДGE=AEЉAG=![]() ЃЌдђЁїOPPЁфгыЁїOGEЕФУцЛ§жЎБШ=
ЃЌдђЁїOPPЁфгыЁїOGEЕФУцЛ§жЎБШ=![]() ЁС
ЁС![]() ЁС
ЁС![]() ЃК
ЃК![]() ЁС
ЁС![]() ЁС
ЁС![]() ЁС
ЁС![]() =25ЃК7.
=25ЃК7.
ЃЈ1ЃЉЁпBDЁЭACЃЌ
ЁрЁЯADB=90ЁуЃЌ
ЁпЁЯABC=90ЁуЃЌ
ЁрЁЯC+ЁЯA=90ЁуЃЌЁЯA+ЁЯABD=90ЁуЃЌ
ЁрЁЯA=ЁЯABDЃЌ
ЁрsinЁЯC=sinЁЯABD=![]() =
=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2жаЃЌСЌНгGF,
дкRtЁїABDжаЃЌBD=![]() =3ЃЌ
=3ЃЌ
ЁпBGЪЧжБОЖЃЌ
ЁрЁЯBFG=ЁЯAFG=90ЁуЃЌ
ЁрsinA=![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЁрFG=![]() ЃЌ
ЃЌ
ЁпDG=ADЉAG=4Љ![]() =
=![]() ЃЌ
ЃЌ
ЁрGD=GFЃЌ
ЁрЁЯEPG=ЁЯFPGЃЛ
ЃЈ3ЃЉЂйШчЭМ3жаЃЌЕБЁбOгыBCЯрЧаЪБЃЌзїOHЁЭABгкHЃЌ
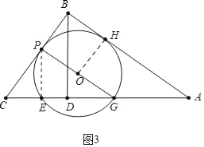
ЁпЁЯOPB=ЁЯPBH=ЁЯOHB=90ЁуЃЌ
ЁрЫФБпаЮPBHOЪЧОиаЮЃЌ
ЁпЁЯC+ЁЯA=90ЁуЃЌЁЯDBA+ЁЯA=90ЁуЃЌ
ЁрЁЯC=ЁЯABDЃЌЁпЁЯBDC=ЁЯBDAЃЌ
ЁрЁїBDCЁзЁїADBЃЌ
ЁрBD2=CDADЃЌ
ЁрCD=![]() ЃЌ
ЃЌ
ЁрBC=![]() =
=![]() ЃЌ
ЃЌ
ЁпBCЪЧЧаЯпЃЌ
ЁрGPЁЭBCЃЌ
ЁрGPC=ЁЯABC=90ЁуЃЌ
ЁрGPЁЮABЃЌ
ЁрЁЯCGP=ЁЯAЃЌ
ЁрsinЁЯA=sinЁЯPGCЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ЁрPC=![]() ЃЌ
ЃЌ
ЁрPB=BCЉPC=![]() ЃЌ
ЃЌ
ЁрPG=![]() =3ЃЌ
=3ЃЌ
ЁрOH=PB=![]() ЃЌ
ЃЌ
ЁрДЫЪБЁбOгыABЯрЧаЃЌСЌНгPEЃЌ
ЁпPGЪЧЁбOЕФжБОЖЃЌ
ЁрЁЯPEG=90ЁуЃЌ
ЁрЁЯPEC=ЁЯCDB=90ЁуЃЌ
ЁрPEЁЮBDЃЌ
ЁрDEЃКCD=PBЃКBCЃЌ
ЁрDEЃК![]() =
=![]() ЃК
ЃК![]() ЃЌ
ЃЌ
ЁрDE=![]() ЃЛ
ЃЛ
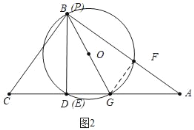
ШчЭМ4жаЃЌЕБЕуPдкABЩЯЃЌЁбOгыBCЯрЧаЪБЃЌЩшЧаЕуЮЊTЃЌСЌНгOTЃЌGHЃЌбгГЄTOНЛGHгкNЃЌСЌНгPEЃЌ
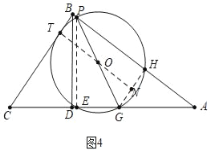
взжЄЫФБпаЮBTNHЪЧОиаЮЃЌ
гЩЃЈ1ЃЉПЩжЊЃКGH=![]() ЃЌAH=2ЃЌBH=3ЃЌGN=NH=
ЃЌAH=2ЃЌBH=3ЃЌGN=NH=![]() ЃЌЩшOT=OG=mЃЌ
ЃЌЩшOT=OG=mЃЌ
дкRtЁїOGNжаЃЌЁпOG2=ON2+GN2ЃЌ
Ёрm2=ЃЈ3ЉmЃЉ2+ЃЈ![]() ЃЉ2ЃЌ
ЃЉ2ЃЌ
Ёрm=![]() ЃЌ
ЃЌ
ЁрON=![]() ЃЌ
ЃЌ
ЁпOG=OPЃЌGN=NHЃЌ
ЁрPH=2ON=![]() ЃЌ
ЃЌ
ЁрPA=PH+AH=![]() ЃЌ
ЃЌ
ЁпPEЁЮBDЃЌ
Ёр![]() =
=![]() ЃЌМД
ЃЌМД![]() =
=![]() ЃЌ
ЃЌ
ЁрAE=![]() ЃЌ
ЃЌ
ЁрDE=ADЉAE=4Љ![]() =
=![]() ЃЛ
ЃЛ
ШчЭМ5жаЃЌЕБЁбOгыABЯрЧаЪБЃЌGPЁЭABЃЌСЌНгPHЃЌ
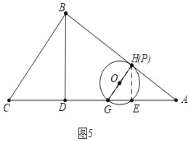
ЁпHEЁЭAGЃЌ
ЁрЁЯPEG=ЁЯAPG=90ЁуЃЌЁпЁЯAGP=ЁЯPGEЃЌ
ЁрЁїPGEЁзЁїAGHЃЌ
ЁрPG2=GEGAЃЌ
ЁрGE=![]() ЃЌ
ЃЌ
ЁрDE=DG+GE=![]() +
+![]() =
=![]() ЃЛ
ЃЛ
злЩЯЫљЪіЃЌЕБBCЛђABгыЁбOЯрЧаЪБЃЌТњзуЬѕМўЕФDEГЄЮЊ![]() Лђ
Лђ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЂкШчЭМ3жаЃЌгУЃЈ2ЃЉПЩжЊЃЌЕуPвддВаФOЮЊа§зЊжааФЃЌЫГЪБеыЗНЯђа§зЊ90ЁуЕУЕНPЃЌ
ЕБPЧЁКУТфдкABБпЩЯЪБЃЌ
ДЫЪБЁїOPPЁфгыЁїOGEЕФУцЛ§жЎБШ=![]() ЁС
ЁС![]() ЁС
ЁС![]() ЃК
ЃК![]() ЁС
ЁС![]() ЁС
ЁС![]() ЁС
ЁС![]() =25ЃК24ЃЛ
=25ЃК24ЃЛ
ШчЭМ6жаЃЌЕБЁїPOHЪЧЕШбќжБНЧШ§НЧаЮЪБЃЌТњзуЬѕМўЃЛ
СЌНгPEЃЌ
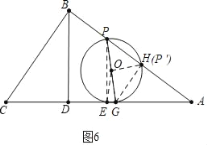
ЁпPH=GH=![]() ЃЌAH=2ЃЌ
ЃЌAH=2ЃЌ
ЁрPA=![]() ЃЌOP=OH=
ЃЌOP=OH=![]() ЃЌ
ЃЌ
ЁпPEЁЮBDЃЌ
ЁрPAЃКAB=AEЃКAD=PEЃКBDЃЌ
Ёр![]() ЃК5=AEЃК4=PEЃК3ЃЌ
ЃК5=AEЃК4=PEЃК3ЃЌ
ЁрAE=![]() ЃЌPE=
ЃЌPE=![]() ЃЌ
ЃЌ
ЁрGE=AEЉAG=![]() ЃЌ
ЃЌ
ЁрЁїOPPЁфгыЁїOGEЕФУцЛ§жЎБШ=![]() ЁС
ЁС![]() ЁС
ЁС![]() ЃК
ЃК![]() ЁС
ЁС![]() ЁС
ЁС![]() ЁС
ЁС![]() =25ЃК7ЃЛ
=25ЃК7ЃЛ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЁїOPPЁфгыЁїOGEЕФУцЛ§жЎБШЮЊ25ЃК24Лђ25ЃК7ЃЎ