题目内容
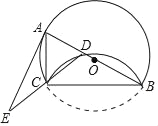
【题目】如图,△ABC内接于⊙O,且AB=BC.AD是⊙O的直径,AC、BD交于点E,P为DB延长线上一点,且PB=BE.
(1)求证:△ABE∽△DBA;
(2)试判断PA与⊙O的位置关系,并说明理由;
(3)若E为BD的中点,求tan∠ADC的值.

【答案】(1)证明见解析;(2)PA与⊙O相切,理由见解析;(3)2![]() .
.
【解析】
分析: (1)先判断出弧AB=弧BC,进而得出∠ADB=∠BAE,即可得出结论;
(2)先判断出AB是PE的垂直平分线,进而得出∠BAP=∠BAE,即可得出结论;
(3)先利用相似得出AB,进而用勾股定理的粗话AE,再判断出△ABE∽△DCE,进而求出CD,CE,即可得出AC,即可得出结论.
详解:
(1)证明:∵AB=BC,
∴![]() ,
,
∴∠ADB=∠BAE,
∵∠ABE=∠DBA,
∴△ABE∽△DBA;
(2)解:PA与⊙O相切,
理由:∵AD是⊙O的直径,
∴∠ABD=90°,
∵PB=BE,
∴AB是PE的垂直平分线,
∴AP=AE,
∴∠BAP=∠BAE,
∵∠ADB=∠BAE,
∴∠BAP=∠ADB,
∵∠DAB+∠BDA=90°,
∴∠DAB+BAP=90°,
∵点A在⊙O上,
∴PA与⊙O相切;
(3)解:设BE=DE=a,则BD=2a,
∵△ABE∽△DBA,
∴![]() ,
,
∴![]() ,
,
∴AB=![]() a,
a,
根据勾股定理得,AE=![]() =
=![]() a,
a,
∵![]() ,
,
∴∠BAE=∠CDE,
∵∠AEB=∠DEC,
∴△ABE∽△DCE,
∴![]() ,
,
∴![]() ,
,
∴CD=![]() a,CE=
a,CE=![]() a,
a,
∴AC=AE+CE=![]() ,
,
∵AD是⊙O直径,
∴∠ACD=90°,
在Rt△ACD中,tan∠ADC=![]() =2
=2![]() .
.

练习册系列答案
相关题目