题目内容
【题目】在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 平分
平分![]() .
.
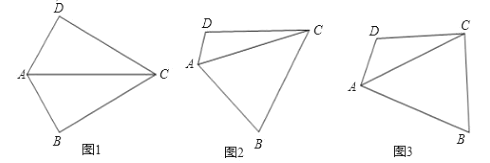
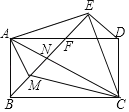
(1)如图1,若![]() ,且
,且![]() ,直接写出线段
,直接写出线段![]() 、
、![]() 、
、![]() 的数量关系.
的数量关系.
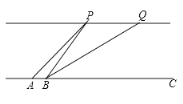
(2)如图2,若将(1)中的条件“![]() ”去掉,求边
”去掉,求边![]() 、
、![]() 与对角线
与对角线![]() 的数量关系.请证明.
的数量关系.请证明.
(3)如图3,若![]() ,直接写出边
,直接写出边![]() 、
、![]() 与对角线
与对角线![]() 的数量关系(用
的数量关系(用![]() 来表示)
来表示)
【答案】(1)AB+AD=AC;(2)AC= AB+AD;(3)AB+AD=2![]() .
.
【解析】
(1)先计算出∠D=![]() ,∠CAB=∠CAD=60°,得到AC=2AB,AC=2AD,由此得到AB+AD=AC;
,∠CAB=∠CAD=60°,得到AC=2AB,AC=2AD,由此得到AB+AD=AC;
(2)以点C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,证明△ACE是等边三角形,再证△ACD≌△ECB,即可得到AC=AD+AB;
(3)过点C作∠BCE=∠ACD,证明∠E=∠CAE得到△ACD≌△ECB,过点C作CF⊥AE于F,得到AF=![]() ,即可得到AB+AD=2
,即可得到AB+AD=2![]() .
.
(1)∵![]() ,
,![]() ,
,
∴∠D=![]() ,
,
∵![]() ,对角线
,对角线![]() 平分
平分![]() ,
,
∴∠CAB=∠CAD=60°,
∴AC=2AB,AC=2AD,
∴AB+AD=AC;
(2)以点C为顶点,AC为一边作∠ACE=60°,∠ACE的另一边交AB延长线于点E,
∵∠DAB=120°,![]() ,
,
∴∠DCB=60°,
∵∠BAC=60°,
∴△ACE是等边三角形,
∴AC=AE=CE,∠ACE=60°,
∴∠ACD=∠BCE,
∵![]() ,∠ABC+∠CBE=180°,
,∠ABC+∠CBE=180°,
∴∠D=∠CBE,
∴△ACD≌△ECB,
∴AD=BE,
∴AC=AD+AB;
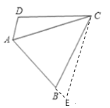
(3)过点C作∠BCE=∠ACD,
∵![]() ,∠ABC+∠CBE=180°,
,∠ABC+∠CBE=180°,
∴∠D=∠CBE,
∴∠E=∠CAD=![]() ∠DAB=
∠DAB=![]() ,
,
∵∠CAB=![]() ∠DAB=
∠DAB=![]() ,
,
∴∠E=∠CAE,
∴AC=CE,
∴△ACD≌△ECB,
∴AD=BE,
过点C作CF⊥AE于F,
∴2AF=AB+BE=AB+AD,
∵AF=![]() ,
,
∴2AF=2![]() ,
,
∴AB+AD=2![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案【题目】某校计划购进甲、乙两种规格的书架,经市场调查发现有线上和线下两种购买方式,具体情况如下表:
规格 | 线下 | 线上 | ||
单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
甲 | 240 | 0 | 210 | 20 |
乙 | 300 | 0 | 250 | 30 |
(1)如果在线下购买甲、乙两种书架共30个,花费8280元,求甲、乙两种书架各购买了多少个?
(2)如果在线上购买甲、乙两种书架共30个,且购买乙种书架的数量不少于甲种书架的3倍,请求出花费最少的购买方案及花费.