题目内容
【题目】已知二次函数y=
（k是常数）．
（1）若该函数的图象与x轴有两个不同的交点，试求k的取值范围；
（2）若点（1，k）在某反比例函数图象上，要使该反比例函数和二次函数y=都是y随x的增大而增大，求k应满足的条件及x的取值范围；
（3）若抛物线y=与x轴交于A（
，0）、B（
，0）两点，且＜，
=34，若与y轴不平行的直线y=ax+b经过点P（1，3），且与抛物线交于
（
，
）、
（
，
）两点，试探究
是否为定值，并写出探究过程．
【答案】(1) k＜
，且k≠0；(2) k＜0；x＜
；(3)1，理由详见解析.
【解析】
试题分析：（1）根据题意k≠0，△＞0，列出不等式组即可解决问题．
（2）设反比例函数解析式为y=
，因为经过点（1，k），所以m=k，再根据条件即可确定k的值以及x的范围．
（3）结论：
=1．令y=0，则有
=0，所以
+
=
，
=
，根据
=34，列出方程求出k的值，设过点P的直线为y=kx+3﹣k，由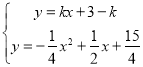
消去y得
+（4k﹣2）x﹣3﹣4k=0，得
=﹣（4k﹣2），
=﹣3﹣4k，根据=
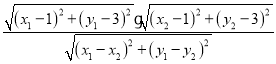，代入化简即可解决问题．
试题解析：（1）∵二次函数y=与x轴有两个不同的交点，
∴
，
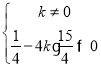解得k＜，且k≠0．
所以若该函数的图象与x轴有两个不同的交点，k的取值范围是k＜，且k≠0；
（2）设反比例函数解析式为y=，
∵经过点（1，k），
∴m=k，
∵反比例函数和二次函数y=都是y随x的增大而增大，
∴k＜0，x＜
，即x＜．
（3）结论：=1．
理由：令y=0，则有=0，
∴+=，=
∵=34，
∴
=34，
∴
=0，
解得k=
或
，
由（1）可知k＜，
∴k=，
∴抛物线解析式为y=
，
设过点P的直线为y=kx+b，把P（1，3）代入得3=k+b，
∴b=3﹣k，
∴过点P的直线为y=kx+3﹣k，
∵过点P的直线为y=kx+3﹣k与物线交于
（
，
）、
（
，
）两点，
∴=k+3﹣k，=k+3﹣k，
由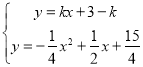消去y得+（4k﹣2）x﹣3﹣4k=0，
∴=﹣（4k﹣2），=﹣3﹣4k ，
∴==
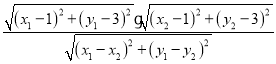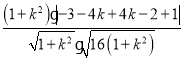=1.
