题目内容
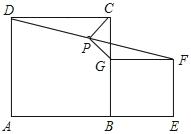
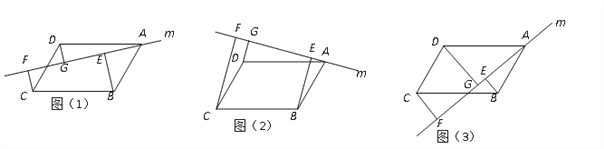
【题目】已知□ABCD中,直线m绕点A旋转,直线m不经过B、C、D点,过B、C、D分别作BE⊥m于E, CF⊥m于F, DG⊥m于G.
(1)当直线m旋转到如图1位置时,线段BE、CF、DG之间的数量关系是 _;
(2)当直线m旋转到如图2位置时,线段BE、CF、DG之间的数量关系是 _;
(3)当直线m旋转到如图3的位置时,线段BE、CF、DG之间有怎样的数量关系?请直接写出你的猜想,并加以证明.
【答案】见解析
【解析】解:
(1)如图1,过C作CM⊥DG,交DG的延长线于点M,

∵DM⊥CM,CF⊥AF,CM⊥DG,
∴∠DMC=∠CFG=∠AEB=90°,
∴四边形GFCM为矩形,
∴FG∥CM,FC=GM,
∵四边形ABCD为平行四边形,
∴CD=AB,CD∥AB,
∴∠DOG=∠BAE=∠DCM,
在△CDM和△ABE中
![]()
∴△CDM≌△ABE(AAS),
∴DM=BE,
∴BE=DG+GM=CF+DG,
故答案为:BE=CF+DG;
(2)如图2,过D作DN⊥CF,交CF于点N,延长CD交AF于点P,
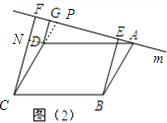
∵DG⊥AF,CF⊥AF,
∴四边形DGFN为矩形,
∴ND∥AF,且DG=NF,
∵四边形ABCD为平行四边形,
∴AB=CD,且AB∥CD,
∴∠CDN=∠DPG=∠BAE,
在△CDN和△BAE中
![]()
∴△CDN≌△BAE(AAS),
∴CN=BE,
∴CF=CN+DF=BE+DG,
故答案为:CF=BE+DG;
(3)猜想:DG=BE+CF;
证明:如图3,过C作CH⊥DG于H,
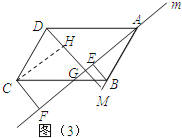
又∵CF⊥m,DG⊥m,
∴四边形CFGH是矩形,
∴CF=HG,
∵DG⊥m,BE⊥m,
∴∠DGE=∠BEG=90°,
∴DG∥BE,
∴∠ABE=∠AMG
∵□ABCD,
∴AD∥BC,CD=AB,
∴∠CDH=∠AMG,
∴∠CDH=∠ABE,
在△CDH和△ABE中
![]()
∴△CDH≌△ABE(AAS),
∴DH=BE,
∴DG=DH+HG=BE+CF,
∴DG=BE+CF.