��Ŀ����
����Ŀ���Ķ����в��ϣ�
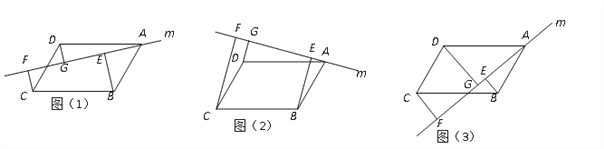
���⣺��ͼ��ʾ����������ABCD��BEFG�У���A��B��E��ͬһֱ���ϣ�P���߶�DF�е㣬����PG��PC��
̽������PG��PC�ļн�Ϊ90��ʱ��ƽ���ı���BEFG�������Σ�
С��ͬѧ��˼·�ǣ����ȿ���֤���ı���BEFG�Ǿ��Σ�Ȼ���ӳ�GP��DC�ڵ�H������ȫ�������Σ�������������̽��������𰸣�
����ο�С��ͬѧ��˼·��̽�������������⣮
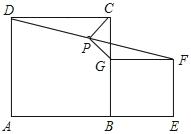
��1����֤���ı���BEFG�Ǿ��Σ�
��2����֤��PG��PC�ļн�Ϊ90��ʱ���ı���BEFG�������Σ�
���𰸡�������
��������֤������1����������ABCD�У���ABC=90�㣬
���EBG=90�㣬
���ı���BEFG��ƽ���ı��Σ�
��ƽ���ı���BEFG�Ǿ��Σ�
��2����ͼ��
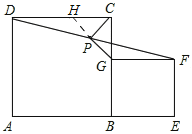
�ӳ�GP��DC�ڵ�H��
����������ABCD��BEFG��
��AB��DC��RE��GF��
��DC��GF��
���HDP=��GFP����DHP=��FGP��
����P���߶�DF�е㣬
��DP=FP��
���DHP�ա�FGP��
��DH=FG��HP=GP��
�ߡ�CPG=90�㣬
��CH=CG��
��������ABCD��DC=BC��
��DH=BG��
��BG=GF��
�ɣ�1��֪���ı���BEFG�Ǿ��Σ�
���ı���BEFG�������Σ�

����Ŀ���ס�������ˮ������������5���ƽ����λ����������£�����λ����/���꣩
Ʒ�� | ��1�� | ��2�� | ��3�� | ��4�� | ��5 �� |
�� | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
�� | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
��1������ˮ����ƽ����λ��������Ƚϸߣ�
��2������ˮ���IJ����Ƚ��ȶ���