题目内容
如图,
是半圆的直径,
为圆心,
、
是半圆的弦，且
.
(1)判断直线
是否为⊙O的切线，并说明理由；
(2)如果
，
，求
的长.
是半圆的直径,为圆心,、是半圆的弦，且.(1)判断直线
是否为⊙O的切线，并说明理由；(2)如果
，，求的长.（1）PD是⊙O的切线（2） PA="1"
试题分析：（1）
是半圆的直径,为圆心,、是半圆的弦，则
，所以
；因为OA=OD，所以
，又因为，所以
，即OD⊥PD，因为OD是圆的直径，所以PD是⊙O的切线（2）根据圆的性质，
，因为，所以
，又因为OA=OD，所以三角形OAD是等边三角形，所以
；由（1）知
，在三角形PDO中，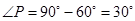
，根据直角三角形的性质，PO=2OD，所以PA=OA=OD；因为，由勾股定理得PA=1点评：本题考查直线与圆相切、勾股定理，要求考生掌握勾股定理的内容，会判定直线与圆的位置关系，会判定直线与圆相切
练习册系列答案
相关题目
cm B．
cm D．
cm
的扇形围成一个圆锥的侧面（接缝忽略不计），则这个圆锥的底面半径是（ ）．
，两圆的半径分别是方程
的两个根，则两圆的位置关系是_____．