题目内容

若两圆的圆心距为，两圆的半径分别是方程的两个根，则两圆的位置关系是_____．
相交

试题分析：根据一元二次方程根与系数的关系可得两圆的半径之和为4，再结合两圆的圆心距为根据圆与圆的位置关系即可作出判断.
由题意得两圆的半径之和为4
∵两圆的圆心距为
∴两圆的位置关系是相交．
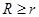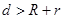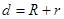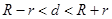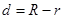点评：若两圆的半径分别为R和r，且，圆心距为d：外离，则；外切，则；相交，则；内切，则；内含，则．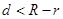
练习册系列答案
相关题目
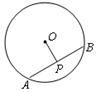
如图，点P是半径为5的⊙O内的一点，且OP＝3，设AB是过点P的 ⊙O内的弦，且AB⊥OP，则弦AB长是________．
如图,是半圆的直径,为圆心,、是半圆的弦，且.

(1)判断直线是否为⊙O的切线，并说明理由；
(2)如果，，求的长.
如图，⊙P与y轴相切，圆心为P（－2，1），直线MN过点M（2，3），N（4，1）.
（1）请你在图中作出⊙P关于y轴对称的⊙P′；（不要求写作法）
  
（2）求⊙P在轴上截得的线段长度；
（3）直接写出圆心P′到直线MN的距离．
在半径为6的圆中，60°的圆心角所对的弧长等于　    ．
如图，△ABC内接于⊙O, AD是⊙O直径, E是CB延长线上一点, 且ÐBAE=ÐC.

（1）求证：直线AE是⊙O的切线；
（2）若EB="AB" , ,  AE=24，求EB的长及⊙O的半径。
如图，在△ABC中，∠A＝∠B＝30°，过点C作CD⊥AC，交AB于点D．
  
（1）作⊙O，使⊙O经过A、C、D三点（尺规作图，保留作图痕迹，不写作法）；
（2）判断直线 BC与⊙O的位置关系，并说明理由．
在△ABC中，∠A=90°，AB=4，AC=3，M是AB上的动点（不与A、B重合），过M作MN//BC交AC于点N，以MN为直径作⊙O，设AM=x

（1）用含x的代数式表示△AMN的面积S；
（2）M在AB上运动，当⊙O与BC相切时（如图①），求x的值；
（3）M在AB上运动，当⊙O与BC相交时（如图②），在⊙O上取一点P，使PM//AC，连接PN，PM交BC于E，PN交BC于点F，设梯形MNFE的面积为y，求y关于x的函数关系式。
如图，圆锥的底面半径为3cm，高为4cm，那么这个圆锥的侧面积是       cm2。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网