题目内容
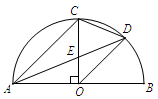
如图,⊙O的直径AB垂直于弦CD,垂足为H,点P是弧AC上的一点(点P不与A,C重合),连结PC,PD,PA,AD,点E在AP的延长线上,PD与AB交于点F.给出下列四个结论:①CH2=AH·BH;②弧AD=弧AC;③AD2=DF·DP;④∠EPC=∠APD.
其中正确的个数有

A.1个 B.2个 C.3个 D.4个
其中正确的个数有

A.1个 B.2个 C.3个 D.4个
C
试题分析:连接AC、BC;⊙O的直径AB垂直于弦CD,垂足为H,
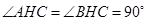 ,
,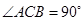 ,
,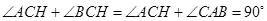 ,所以
,所以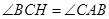 ,因此可得
,因此可得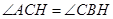 ,所以在
,所以在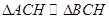 ,
,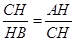 ,所以CH2=AH·BH,①正确;⊙O的直径AB垂直于弦CD,垂足为H,根据弦心矩的性质,所以弧AD=弧AC,②正确;如图,⊙O的直径AB垂直于弦CD,垂足为H,点P是弧AC上的一点(点P不与A,C重合),连结PC,PD,PA,AD,点E在AP的延长线上,PD与AB交于点F,可证
,所以CH2=AH·BH,①正确;⊙O的直径AB垂直于弦CD,垂足为H,根据弦心矩的性质,所以弧AD=弧AC,②正确;如图,⊙O的直径AB垂直于弦CD,垂足为H,点P是弧AC上的一点(点P不与A,C重合),连结PC,PD,PA,AD,点E在AP的延长线上,PD与AB交于点F,可证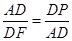 ,所以AD2=DF·DP,因此③正确;由②知弧AD=弧AC,所以
,所以AD2=DF·DP,因此③正确;由②知弧AD=弧AC,所以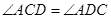 ,
,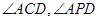 是弧AD所对的圆周角,所以
是弧AD所对的圆周角,所以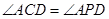 ,因此
,因此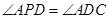 ,根据题意
,根据题意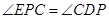 ,而
,而 分别是弧PC,弧AC所对的圆周角,因为弧PC小于弧AC,所以
分别是弧PC,弧AC所对的圆周角,因为弧PC小于弧AC,所以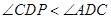 ,因此
,因此 ,所以④错误
,所以④错误点评:本题考查弦心距,相似三角形,解本题需要掌握弦心距的性质,熟悉相似三角形的判定方法,会证明两个三角形相似

练习册系列答案
相关题目
 是半圆的直径,
是半圆的直径, 为圆心,
为圆心, 、
、 是半圆的弦,且
是半圆的弦,且 .
.
 是否为⊙O的切线,并说明理由;
是否为⊙O的切线,并说明理由; ,
, ,求
,求 的长.
的长.

 cm2
cm2 cm2
cm2

 和7
和7
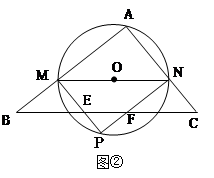
 于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE与CO的比例中项,其中所有正确结论的序号是( )
于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE与CO的比例中项,其中所有正确结论的序号是( )