题目内容
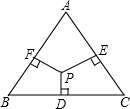
如图，△ABC是等边三角形，P是BC上任意一点，PD⊥AB，PE⊥AC，连接DE．记△ADE的周长为L1，四边形BDEC的周长为L2，则L1与L2的大小关系是（ ）
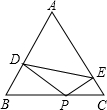
| A．Ll=L2 | B．L1＞L2 | C．L2＞L1 | D．无法确定 |
∵等边三角形各内角为60°，∴∠B=∠C=60°，
∵∠BPD=∠CPE=30°，
∴在Rt△BDP和Rt△CEP中，
∴BP=2BD，CP=2CE，
∴BD+CE=
BC，
∴AD+AE=AB+AC-
BC=
BC，
∴BD+CE+BC=
BC，
L1=
BC+DE，
L2=
BC+DE，
即得L1=L2，
故选 A．
∵∠BPD=∠CPE=30°，
∴在Rt△BDP和Rt△CEP中，
∴BP=2BD，CP=2CE，
∴BD+CE=
| 1 |
| 2 |
∴AD+AE=AB+AC-
| 1 |
| 2 |
| 3 |
| 2 |
∴BD+CE+BC=
| 3 |
| 2 |
L1=
| 3 |
| 2 |
L2=
| 3 |
| 2 |
即得L1=L2，
故选 A．
练习册系列答案
相关题目
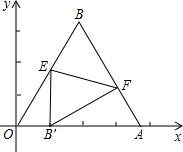正方向上，将△OAB折叠，使点B落在边OA上，记为B′，折痕为EF．
