题目内容
【题目】在
边AB上有一点
（点不与点
、点
重合），过点作直线截
，使截得的三角形与相似，满足条件的直线共有（ ）
A. 2条 B. 3条 C. 4条 D. 5条
【答案】B
【解析】
点P在AB边上，根据相似三角形的判定方法进行分析，即可得到有几条这样的直线．
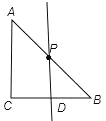
满足条件的直线有3条，如图所示．
第一个，点P在边AB上，过点P作PD∥AC，根据平行于三角形的一边的直线与另一边相交，所构成的三角形与原三角形相似，得到△BPD∽△BAC；
第二个，点P在AB边上，过P作PD∥BC，根据平行于三角形的一边的直线与另一边相交，所构成的三角形与原三角形相似，得到△APD∽△ABC；
第三个，点P在边AB上，过点P作PD⊥AB，根据有两组角对应相等的两个三角形相似，得到△APD∽△ACB；
故选：B．
练习册系列答案
相关题目
