Question

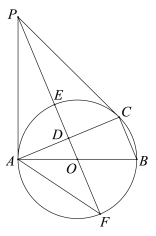
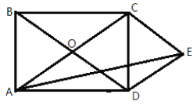
【题目】如图，矩形的对角线、相交于点，AB与BC的比是黄金比，过点C作CE∥BD，过点D作DE∥AC，DE、交于点，连接AE，则tan∠DAE的值为___________.（不取近似值）　

Answer 1

【答案】

【解析】

根据AB与BC的比是黄金比得到AB∶BC=，连接OE与CD交于点G，过E点作EF⊥AF交AD延长线于F，证明四边形CEDO是菱形，得到 ，，即可求出tan∠DAE的值；

解：∵AB与BC的比是黄金比，

∴AB∶BC=

连接OE与CD交于点G，过E点作EF⊥AF交AD延长线于F，

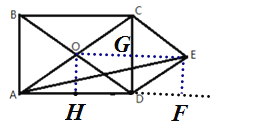
矩形的对角线、相交于点，

∵CE∥BD，DE∥AC，

∴四边形CEDO是平行四边形，

又∵是矩形，

∴OC=OD，

∴四边形CEDO是菱形（邻边相等的平行四边形是菱形），

∴CD与OE垂直且平分，

∴ ，

∴，

tan∠DAE ，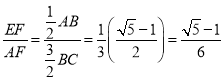

故答案为：；