题目内容
【题目】如图，AB是半圆O的直径，且AB=8，点C为半圆上的一点．将此半圆沿BC所在的直线折叠，若圆弧BC恰好过圆心O，则图中阴影部分的面积是 ． （结果保留π） 
【答案】
【解析】解：过点O作OD⊥BC于点D，交 
于点E，连接OC， 则点E是 
的中点，由折叠的性质可得点O为 
的中点，
∴S弓形BO=S弓形CO ，
在Rt△BOD中，OD=DE= 
R=2，OB=R=4，
∴∠OBD=30°，
∴∠AOC=60°，
∴S阴影=S扇形AOC= 
= ．
故答案为： ．
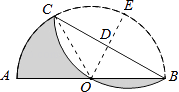
过点O作OD⊥BC于点D，交 于点E，则可判断点O是 的中点，由折叠的性质可得OD= OE= R=2，在Rt△OBD中求出∠OBD=30°，继而得出∠AOC，求出扇形AOC的面积即可得出阴影部分的面积．
练习册系列答案
相关题目
【题目】为增强公民的节约意识，合理利用天然气资源，某市自1月1日起对市区民用管道天然气价格进行调整，实行阶梯式气价，调整后的收费价格如表所示：
每月用气量 | 单价（元/m3） |
不超出75m3的部分 | 2.5 |
超出75m3不超出125m3的部分 | a |
超出125m3的部分 | a+0.25 |
（1）若甲用户3月份的用气量为60m3 ， 则应缴费元；
（2）若调价后每月支出的燃气费为y（元），每月的用气量为x（m3），y与x之间的关系如图所示，求a的值及y与x之间的函数关系式；
（3）在（2）的条件下，若乙用户2、3月份共用气175m3（3月份用气量低于2月份用气量），共缴费455元，乙用户2、3月份的用气量各是多少？
