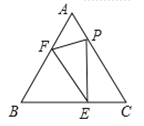
题目内容
【题目】如图,等边![]() 的边长为
的边长为![]() ,
,![]() 是边
是边![]() 上的动点,
上的动点,![]() 交边
交边![]() 于点
于点![]() ,在边
,在边![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)请直接写出图中与线段![]() 相等的两条线段;(不再另外添加辅助线)
相等的两条线段;(不再另外添加辅助线)
(2)探究:当点![]() 在什么位置时,四边形
在什么位置时,四边形![]() 是平行四边形?并判断四边形
是平行四边形?并判断四边形![]() 是什么特殊的平行四边形,请说明理由;
是什么特殊的平行四边形,请说明理由;
(3)在(2)的条件下,以点![]() 为圆心,
为圆心,![]() 为半径作圆,根据
为半径作圆,根据![]() 与平行四边形
与平行四边形![]() 四条边交点的总个数,求相应的
四条边交点的总个数,求相应的![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)由平行易得△BFE是等边三角形,那么各边是相等的;
(2)当点E是BC的中点时,△PEC为等边三角形,可得到PC=EC=BE=EF,也就得到了四边形EFPC是平行四边形,再有EF=EC可证为菱形;
(3)根据各点到圆心的距离作答即可.
解:(1)如图,∵△ABC是等边三角形,
∴∠B=∠A=∠C=60°.
又∵EF∥AC,
∴∠BFE=∠A=60°,∠BEF=∠C=60°,
∴△BFE是等边三角形,PE=EB,
∴EF=BE=PE=BF;
(2)当点E是BC的中点时,四边形是菱形;
∵E是BC的中点,
∴EC=BE,
∵PE=BE,
∴PE=EC,
∵∠C=60°,
∴△PEC是等边三角形,
∴PC=EC=PE,
∵EF=BE,
∴EF=PC,
又∵EF∥CP,
∴四边形EFPC是平行四边形,
∵EC=PC=EF,
∴平行四边形EFPC是菱形;
(3)如图所示:
当点E是BC的中点时,EC=1,则NE=ECcos30°=![]() ,
,
当0<r<![]() 时,有两个交点;
时,有两个交点;
当r=![]() 时,有四个交点;
时,有四个交点;
当![]() <r<1时,有六个交点;
<r<1时,有六个交点;
当r=1时,有三个交点;
当r>1时,有0个交点.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目