题目内容
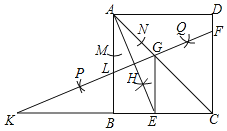
【题目】如图,在正方形ABCD中,连接AC,以点A为圆心,适当长为半径画弧,交AB、AC于点M,N,分别以M,N为圆心,大于MN长的一半为半径画弧,两弧交于点H,连结AH并延长交BC于点E,再分别以A、E为圆心,以大于AE长的一半为半径画弧,两弧交于点P,Q,作直线PQ,分别交CD,AC,AB于点F,G,L,交CB的延长线于点K,连接GE,下列结论:①∠LKB=22.5°,②GE∥AB,③tan∠CGF=![]() ,④S△CGE:S△CAB=1:4.其中正确的是( )
,④S△CGE:S△CAB=1:4.其中正确的是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
【答案】A
【解析】
①在△AOL和△BLK中,根据三角形内角和定理,如图两个角对应相等,则第三个角∠LKB=∠BAC=22.5°;
②根据线段中垂线定理证明∠AEG=∠EAG=22.5°=∠BAE,可得EG∥AB;
③根据等量代换可得:∠CGF=∠BLK,可作判断;
④连接EL,证明四边形ALEG是菱形,根据EL>BL,及相似三角形的性质可作判断.
①∵四边形ABCD是正方形,
∴∠BAC=![]() ∠BAD=45°,
∠BAD=45°,
由作图可知:AE平分∠BAC,
∴∠BAE=∠CAE=22.5°,
∵PQ是AE的中垂线,
∴AE⊥PQ,
∴∠AOL=90°,
∵∠AOL=∠LBK=90°,∠ALO=∠KLB,
∴∠LKB=∠BAE=22.5°;
故①正确;
②∵OG是AE的中垂线,
∴AG=EG,
∴∠AEG=∠EAG=22.5°=∠BAE,
∴EG∥AB,
故②正确;
③∵∠LAO=∠GAO,∠AOL=∠AOG=90°,
∴∠ALO=∠AGO,
∵∠CGF=∠AGO,∠BLK=∠ALO,
∴∠CGF=∠BLK,
在Rt△BKL中,tan∠CGF=tan∠BLK=![]() ,
,
故③正确;
④连接EL,
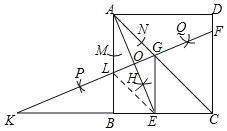
∵AL=AG=EG,EG∥AB,
∴四边形ALEG是菱形,
∴AL=EL=EG>BL,
∴![]() ,
,
∵EG∥AB,
∴△CEG∽△CBA,
∴![]() ,
,
故④不正确;
本题正确的是:①②③,
故选A.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某快递公司计划购买A型和B型两种货车共8辆,其中每辆车的价格以及每辆车的运载量如下表:
A型 | B型 | |
价格(万元/台) | m | n |
运载量(吨/车) | 20 | 30 |
若购买A型货车1辆,B型货车3辆,共需67万元;若购买A型货车3辆,B型货车2辆,共需75万元.
(1)求m,n的值;
(2)若每辆A型货车每月运载量500吨,每辆B型货车每月运载量750吨,为确保这8辆车每月的运载量总和不少于4750吨,且该公司购买A型和B型货车的总费用不超过124万元.请你设计一个方案,使得购车总费用最少.
【题目】背景阅读:
意大利著名数学家裴波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,,其中从第三个数起,每一个数都等于它前面两个数的和.为了纪念这个著名的发现,人们将这组数命名为裴波那契数列.
实践操作:
(1)写出裴波那契数列的前10个数;
(2)裴波那契数列的前2017个数中,有多少个奇数?
(3)现以这组数的各个数作为正方形的边长构造如图1的正方形系列:再分别从左到右取2个、3个、4个、5个正方形拼成如下矩形记为①、②、③、④、⑤……


(i)通过计算相对应长方形的周长填写表(不计拼出的长方形内部的线段)
序号 | ① | ② | ③ | ④ | ⑤ | …… |
周长 | 6 | 10 | …… |
(ii)若按此规律继续拼成长方形,求序号为⑩的长方形的面积和周长.