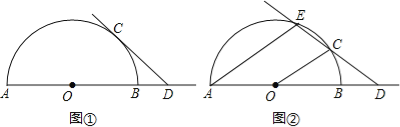Question

【题目】如图，在△ABC中，∠C=90°，以点C为圆心，BC为半径的圆交AB于点D，交AC于点E.

(1)若∠A=25°，求的度数；

(2)若BC=9，AC=12，求BD的长.

Answer 1

【答案】(1)的度数是50°；(2) BD=.

【解析】

（1）求出∠B的度数，求出∠B所对的弧的度数，即可得出答案；

（2）根据勾股定理求出AB，根据割线定理得出比例式，即可得出答案．

(1)延长BC交☉O于点N,

∵在△ABC中,∠C=90°,∠A=25°,∴∠B=65°,

∴∠B所对的弧BDN的度数是130°,

∴的度数是180°-130°=50°.

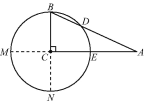
(2)延长AC交☉O于点M,

在Rt△BCA中,由勾股定理得AB==15,

∵BC=9,AC=12,

∴CM=CE=BC=9,AM=AC+CM=21,AE=AC-CE=3,

由割线定理得AD×AB=AE×AM,

∴(15-BD)×15=21×3,解得BD=.