题目内容
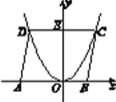
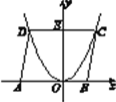
【题目】如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和B(3,0)构成ABCD,DC与y轴的交点为E(0,6),试求a的值.
【答案】![]()
【解析】
由A(-5,0)和B(3,0)得出AB=8,进一步得出CD=AB=8,所以D点的横坐标为-4,再结合E(0,6),得出点D的纵坐标为6,代入D点坐标求得a的数值即可.
解:∵点A(-5,0)和B(3,0),
∴AB=8.
∵四边形ABCD是平行四边形,
∴CD=8,CD∥AB.
又∵AB⊥y轴,抛物线y=ax2的对称轴为y轴,∴CD⊥y轴,
∴DE=![]() CD=4,点D,C,E的纵坐标相同.
CD=4,点D,C,E的纵坐标相同.
又∵点E的坐标为(0,6),
∴点D的坐标为(-4,6).
将D(-4,6)代入y=ax2,
解得a=![]() .
.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
【题目】某快递公司计划购买A型和B型两种货车共8辆,其中每辆车的价格以及每辆车的运载量如下表:
A型 | B型 | |
价格(万元/台) | m | n |
运载量(吨/车) | 20 | 30 |
若购买A型货车1辆,B型货车3辆,共需67万元;若购买A型货车3辆,B型货车2辆,共需75万元.
(1)求m,n的值;
(2)若每辆A型货车每月运载量500吨,每辆B型货车每月运载量750吨,为确保这8辆车每月的运载量总和不少于4750吨,且该公司购买A型和B型货车的总费用不超过124万元.请你设计一个方案,使得购车总费用最少.