题目内容
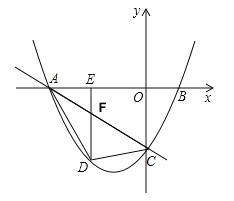
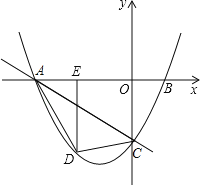
【题目】如图,直线y=-![]() x-3与x轴,y轴分别交于点A,C,经过点A,C的抛物线y=ax2+bx﹣3与x轴的另一个交点为点B(2,0),点D是抛物线上一点,过点D作DE⊥x轴于点E,连接AD,DC.设点D的横坐标为m.
x-3与x轴,y轴分别交于点A,C,经过点A,C的抛物线y=ax2+bx﹣3与x轴的另一个交点为点B(2,0),点D是抛物线上一点,过点D作DE⊥x轴于点E,连接AD,DC.设点D的横坐标为m.
(1)求抛物线的解析式;
(2)当点D在第三象限,设△DAC的面积为S,求S与m的函数关系式,并求出S的最大值及此时点D的坐标;
(3)连接BC,若∠EAD=∠OBC,请直接写出此时点D的坐标.
【答案】(1)y=![]() x2+x﹣3;(2)S△ADC=﹣
x2+x﹣3;(2)S△ADC=﹣![]() (m+3)2+
(m+3)2+![]() ;△ADC的面积最大值为
;△ADC的面积最大值为![]() ;此时D(﹣3,﹣
;此时D(﹣3,﹣![]() );(3)满足条件的点D坐标为(﹣4,﹣3)或(8,21).
);(3)满足条件的点D坐标为(﹣4,﹣3)或(8,21).
【解析】
(1)求出A坐标,再用待定系数法求解析式;(2)设DE与AC的交点为点F.设点D的坐标为:(m,![]() m2+m﹣3),则点F的坐标为:(m,﹣
m2+m﹣3),则点F的坐标为:(m,﹣![]() m﹣3),根据S△ADC=S△ADF+S△DFC求出解析式,再求最值;(3)①当点D与点C关于对称轴对称时,D(﹣4,﹣3),根据对称性此时∠EAD=∠ABC.
m﹣3),根据S△ADC=S△ADF+S△DFC求出解析式,再求最值;(3)①当点D与点C关于对称轴对称时,D(﹣4,﹣3),根据对称性此时∠EAD=∠ABC.
②作点D(﹣4,﹣3)关于x轴的对称点D′(﹣4,3),直线AD′的解析式为y=![]() x+9,解方程组求出函数图像交点坐标.
x+9,解方程组求出函数图像交点坐标.
解:(1)在y=﹣![]() x﹣3中,当y=0时,x=﹣6,
x﹣3中,当y=0时,x=﹣6,
即点A的坐标为:(﹣6,0),
将A(﹣6,0),B(2,0)代入y=ax2+bx﹣3得:
![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:y=![]() x2+x﹣3;
x2+x﹣3;
(2)设点D的坐标为:(m,![]() m2+m﹣3),则点F的坐标为:(m,﹣
m2+m﹣3),则点F的坐标为:(m,﹣![]() m﹣3),
m﹣3),
设DE与AC的交点为点F.
∴DF=﹣![]() m﹣3﹣(
m﹣3﹣(![]() m2+m﹣3)=﹣
m2+m﹣3)=﹣![]() m2﹣
m2﹣![]() m,
m,
∴S△ADC=S△ADF+S△DFC
=![]() DFAE+
DFAE+![]() DFOE
DFOE
=![]() DFOA
DFOA
=![]() ×(﹣
×(﹣![]() m2﹣
m2﹣![]() m)×6
m)×6
=﹣![]() m2﹣
m2﹣![]() m
m
=﹣![]() (m+3)2+
(m+3)2+![]() ,
,
∵a=﹣![]() <0,
<0,
∴抛物线开口向下,
∴当m=﹣3时,S△ADC存在最大值![]() ,
,
又∵当m=﹣3时,![]() m2+m﹣3=﹣
m2+m﹣3=﹣![]() ,
,
∴存在点D(﹣3,﹣![]() ),使得△ADC的面积最大,最大值为
),使得△ADC的面积最大,最大值为![]() ;
;
(3)①当点D与点C关于对称轴对称时,D(﹣4,﹣3),根据对称性此时∠EAD=∠ABC.
②作点D(﹣4,﹣3)关于x轴的对称点D′(﹣4,3),
直线AD′的解析式为y=![]() x+9,
x+9,
由 ,解得
,解得![]() 或
或![]() ,
,
此时直线AD′与抛物线交于D(8,21),满足条件,
综上所述,满足条件的点D坐标为(﹣4,﹣3)或(8,21