Question

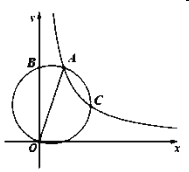
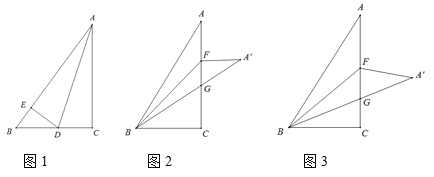
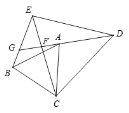
【题目】如图，已知△ABC和△DCE是等边三角形，连接BE，连接DA并延长交CE于点F，交BE于点G，CD=6，EF=2，那么EG的长为__________．

Answer 1

【答案】

【解析】

由等边三角形的性质可得BC=AC，EC=CD=6，∠ACB=∠ECD=60°，由“SAS”可证△ACD≌△BCE，可得∠BEC=∠ADC，EC=DC，根据∠GFE=∠CFD，∠FCD=60°，可得△EGF∽△DCF，则有，可得，设GF=2a，EG=3a，过F作FM⊥EG交EG于M点，在RT△GMF中，利用∠MGF=60°，GF=2a得到GM=a，在RT△EMF中，ME=2a，EF=2，，由勾股定理得，由勾股定理得，即，化简求解即可.

解：

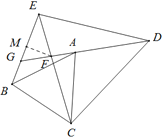
∵△ABC和△DCE是等边三角形，
∴BC=AC，EC=CD=6，∠ACB=∠ECD=60°，
∴∠BAE=∠ACD，且BC=AC，EC=CD，

∴△ACD≌△BCE

∴∠BEC=∠ADC，

∵CD=6；EF=2

∴FC=4

又∵∠GFE=∠CFD；∠FCD=60°

∴△EGF∽△DCF

∴∠EGF=∠FCD=60°且

即

∴设GF=2a，EG=3a；

过F作FM⊥EG交EG于M点

在RT△GMF中，∠MGF=60°，GF=2a

∴GM=a，

∴ME=GE-MG=2a

在RT△EMF中，ME=2a，EF=2，

由勾股定理得

即解得

∴GE=3a=